Research
 My research addresses computational, mathematical, and statistical problems in the study of complex systems, especially social systems. My interests include models of evolving networks; network data science; models with polyadic (higher-order) interactions; methods for quantifying segregation and polarization; and identity representation in academic science. I am especially interested in the interplay between mechanistic dynamical modeling and messy data sets. My research is currently supported by the National Science Foundation grant “RUI: Network Evolution with Unobserved Mechanisms.” For my complete research record, see my Google Scholar page.
My research addresses computational, mathematical, and statistical problems in the study of complex systems, especially social systems. My interests include models of evolving networks; network data science; models with polyadic (higher-order) interactions; methods for quantifying segregation and polarization; and identity representation in academic science. I am especially interested in the interplay between mechanistic dynamical modeling and messy data sets. My research is currently supported by the National Science Foundation grant “RUI: Network Evolution with Unobserved Mechanisms.” For my complete research record, see my Google Scholar page.
I do research with students, typically taking 1-2 students each summer and academic year. I’ve also written down some thoughts on what research students can expect from me and what I expect from them.
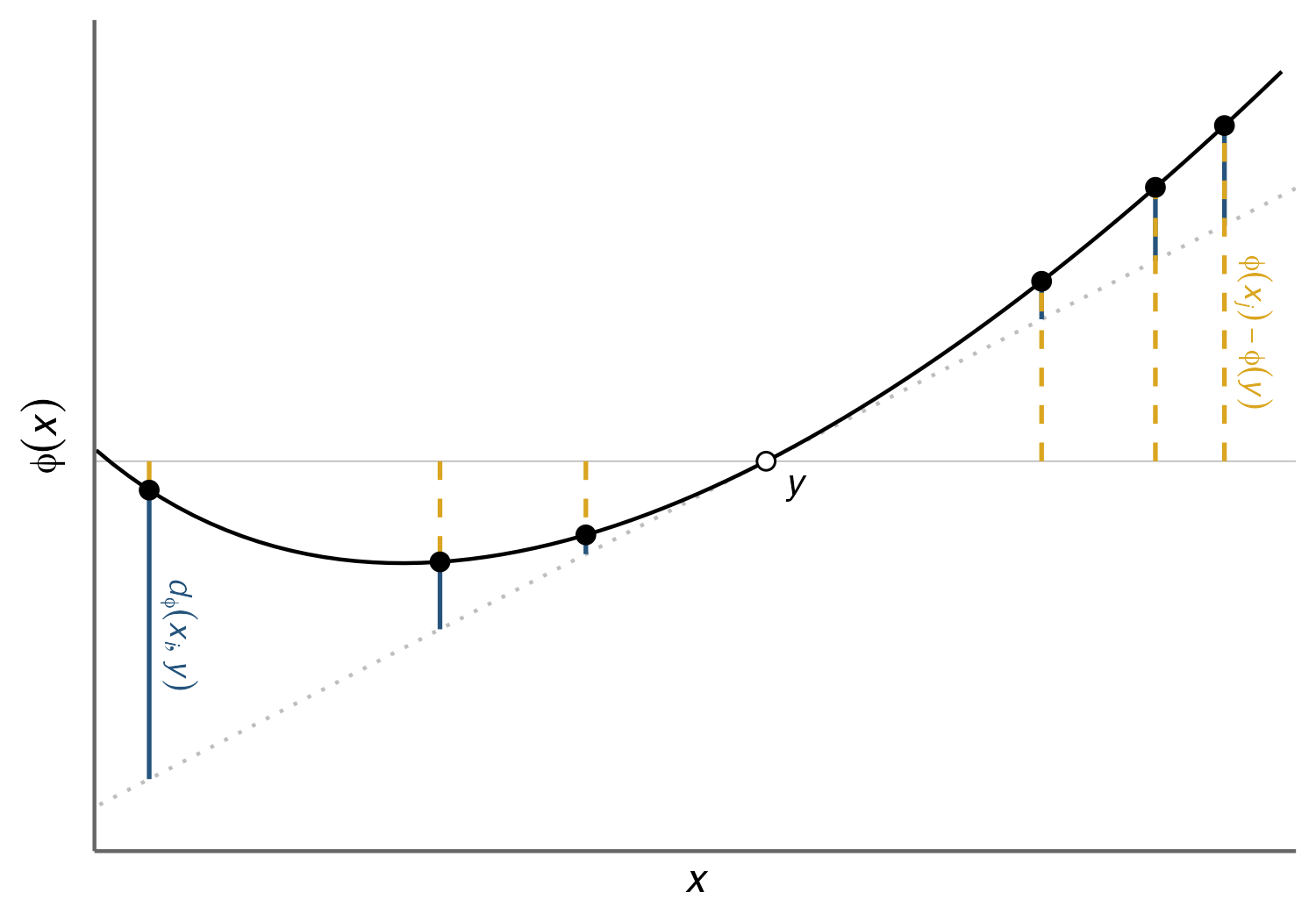
The illustration above is by friend and collaborator Izabel Aguiar.
2025

arXiv preprint arXiv:2502.02386 (2025)
arXiv preprint arXiv:2502.14764 (2025)
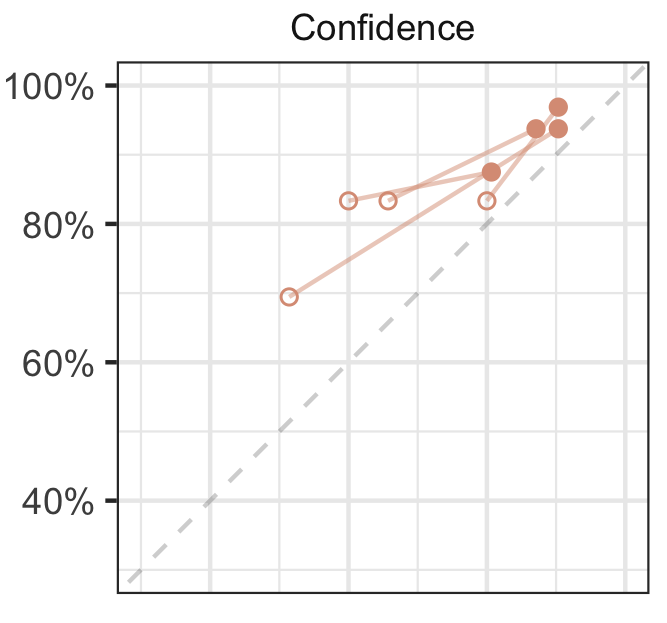
Advances in Data Science: Women in Data Science and Mathematics (WiSDM) 2023 (2025)
2024
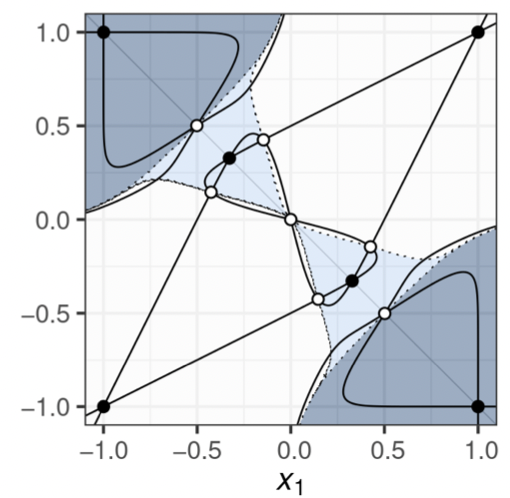
SIAM Journal on Applied of Dynamical Systems (2024)
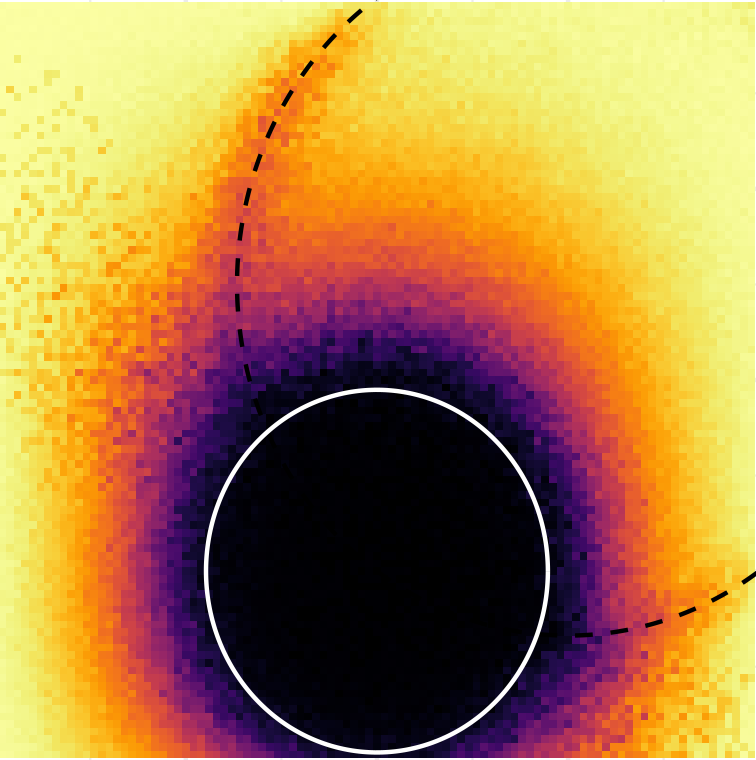
Scientific Reports (2024)
2023
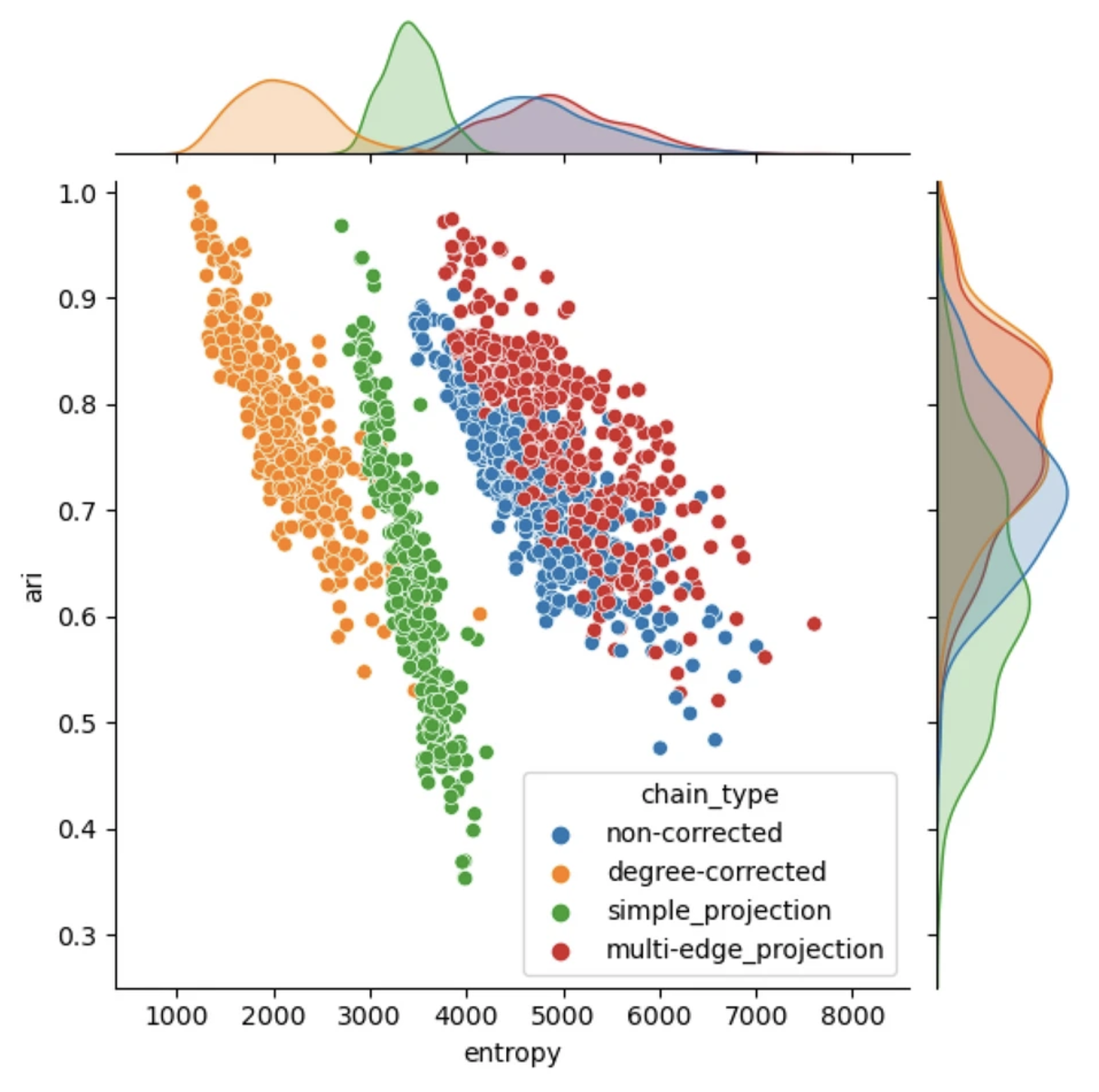
SIAM Journal on Mathematics of Data Science (2023)

Notices of the American Mathematical Society (2023)
2021
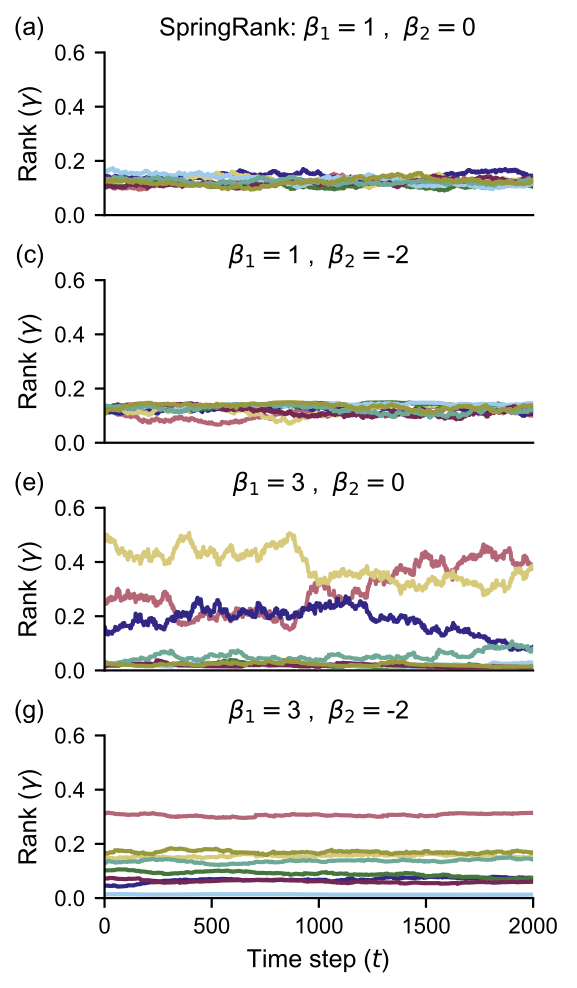
Proceedings of the National Academy of Sciences (2021)
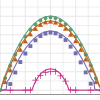
SIAM Journal on Applied Mathematics (2021)
Science Advances (2021)
Geophysics Review Letters (2021)
2020
Journal of Complex Networks (2020)

SIAM Journal on Mathematics of Data Science (2020)
Applied Network Science (2020)
2017
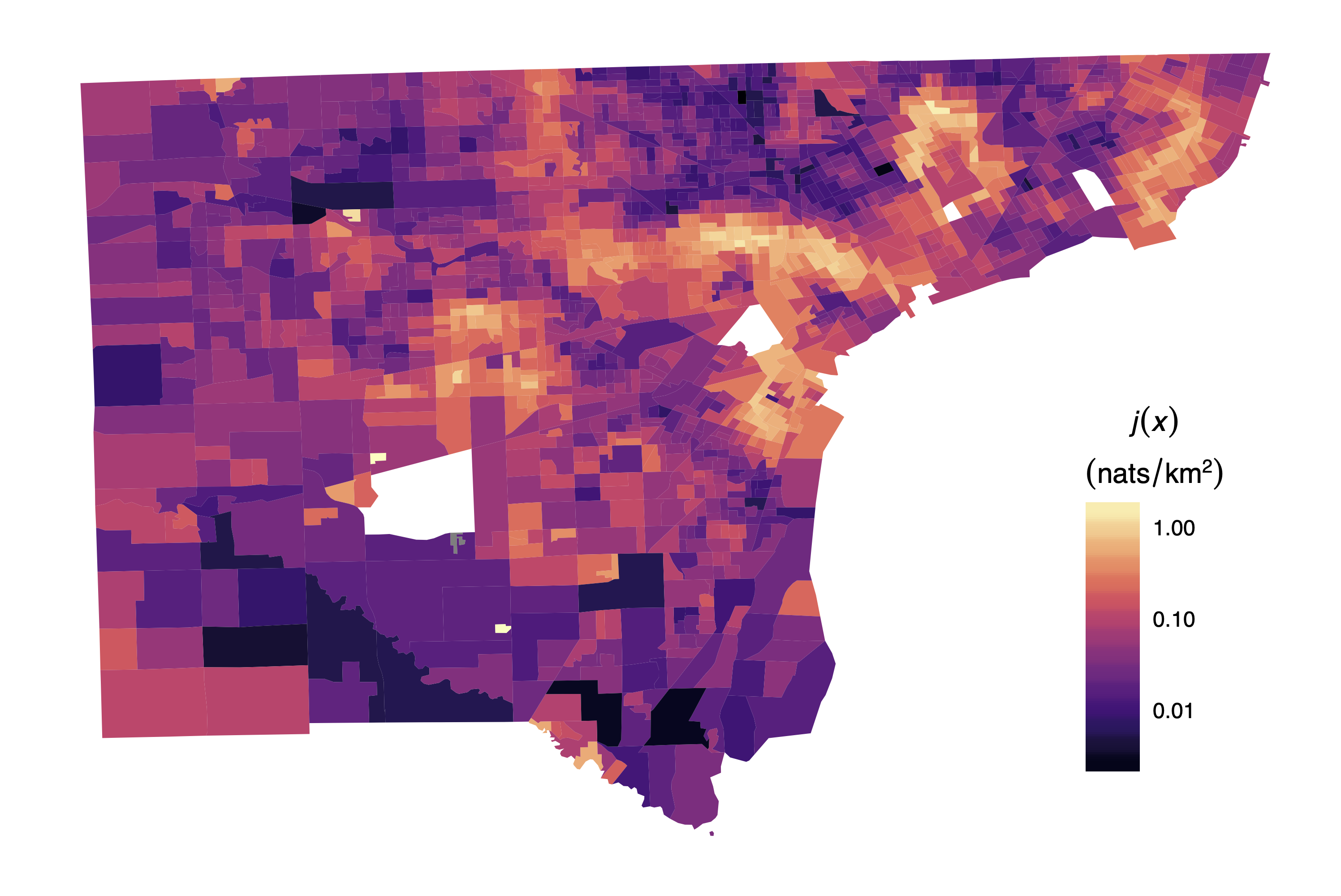
Proceedings of the National Academy of Sciences (2017)