Coevolutionary Graphs

# Coevolutionary Graphs
## Models, Dynamics, and Approximations

---

# Agenda

1). Quick review of some evolutionary graph theory models (for contrast).

2). **Co**evolutionary models and competing timescales.

3). Extended example: approximations for the adaptive voter model.

4). *(The hidden agenda): I want you to work on coevolutionary models.*

---

## Review: **Evolutionary Dynamics on Graphs**

.pull-left[.smaller[1. Choose an individual `$i$` proportional to their current fitness `$\phi_i$`. 
1. Sample `$j \in \mathcal{N}(i)$` proportional to `$w_{ij}$`. Then, `$\phi_j\gets \phi_i$`.
1. .alert[**Isothermal Theorem**]: This process has the same long-term selection dynamics as the complete graph `$K_n$` iff `$T_i = \sum_j{w_{ji}}$` is constant on `$V$`.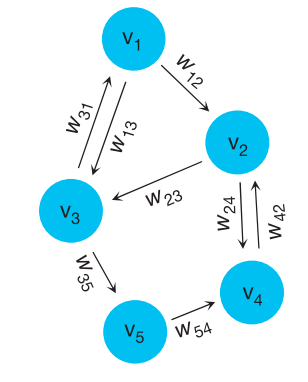 
]
]

---

## Review: **Evolutionary Games on Graphs**

.pull-left[
.smaller[	
1. Agents play a chosen strategy  in a two-player game along each weighted edge.
1. An agent is selected for death, replaced proportional to fitness of neighbors. 
1. .alert[**Result**]: It is possible to classify whether selection favors the emergence of cooperative behavior based purely on graph topology. 
]
]

---

---

background-color: #000000
background-image: url(img/jerks.jpg)
background-size: contain

---

background-color: #000000
background-image: url(img/neighbors.jpg)
background-size: contain

---

background-color: #000000
background-image: url(img/sick.jpg)
background-size: contain

---

class: left, top
background-image: url("img/adaptive_networks.png")
background-size: contain

# Coevolutionary Graphs

.footnote[
Image from Malik and Shi, ["Adaptive Networks in Action"](https://dsweb.siam.org/The-Magazine/Article/adaptive-networks-in-action-opinion-formation-epidemics-and-the-evolution-of-cooperation), *SIAM DS Web*
]

---

# Some Life Advice

"If your friends are jerks, make new friends."

.smaller[.smaller[.smaller[Generic absorbing transition in coevolution dynamics (Vazquez et al.,  *PRL*, 2008)]]]

"If your friends outcompete you, make new friends."

.smaller[.smaller[.smaller[Evolutionary prisoner’s dilemma games coevolving on adaptive networks (Lee et al., *Journal of Complex Networks*, 2017).]]]

"If your friends make you sick, make new friends."

.smaller[.smaller[.smaller[Social clustering in epidemic spread on coevolving networks (Malik et al., *PRE*, 2019).]]]

---

# Mathematically...

---

background-color: #000000
background-image: url(img/borked.jpg)
background-size: contain

---

# Everything is Borked

1) Whole process is usually Markovian, but neither node- nor edge-upates are in isolation `$\rightarrow$` no closed form anything.

2) Edge updates tend to create long-range correlations between node states. `$\rightarrow$` mean-field theories will usually perform poorly.

3) What questions should we even be asking of these models??

---

# Example: Voter Model (AVM)

Nodes have binary states `$\in \{0,1\}$`. 
At each time step `$t$`:

Pick an edge `$e = (u,v)$` where `$u$` and `$v$` disagree.

- With probability `$\alpha$`, .alert[**rewire**]: delete `$(u,v)$` and form `$(u,w)$`, where `$w$` agrees with `$u$` ("rewire-to-same") or `$w$` is uniformly random ("rewire-to-random"). 
- With probability `$1-\alpha$`, .alert[**vote**]: `$v$` adopts `$u$`'s opinion.

**Alternative View**: Neutral drift in a population where wild-types prefer to avoid mutants.

**Alternative Alternative View**: SI model with reactive social distancing.

---

# Let's do an experiment! 
From Malik and Shi, ["Adaptive Networks in Action"](https://dsweb.siam.org/The-Magazine/Article/adaptive-networks-in-action-opinion-formation-epidemics-and-the-evolution-of-cooperation), *SIAM DS Web*

---

class: left, top
background-image: url("img/AVM_animation.gif")
background-size: contain

---

# Model Timescales

With only rewiring ( `$\alpha = 1$` ), disagreement resolved in time `$\sim O(n \log n)$` on sparse graphs. .alert[**Fast dynamics, segregated consensus**].

With only voting ( `$\alpha = 0$` ), disagreement resolved in time `$\sim O(n^2)$`.  .alert[**Slow dynamics, hegemonic consensus**].

These two regimes are separated by a .alert[phase transition] in `$\alpha$`. 
If mean degree is 4, then `$\alpha \approx 0.73$` (rewire-to-random).

---

---

# Near the Phase Transition

---

.bigger[Disparate .alert[**timescales**] between node and edge dynamics drive phase transitions in long-term behavior.]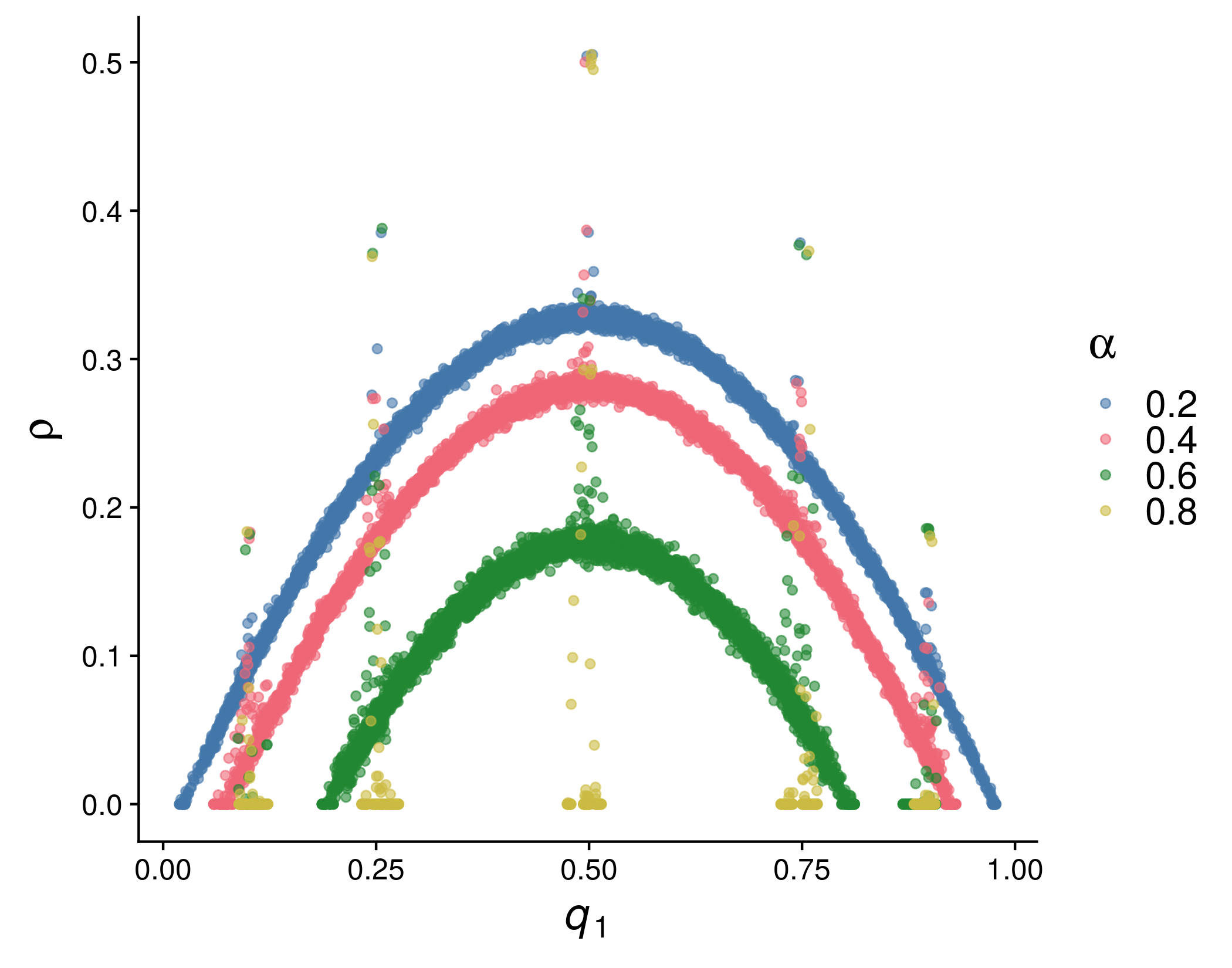

---

# The Arch

.alert[**Quasistable manifold**] governing relationship between fraction of ones `$q_1$` and fraction of discordant edges `$\rho$`. 
]

---

# The Arch: Analysis Questions

.pull-right[
- .alert[**Phase Transition**]: Can we estimate the value of `$\alpha$` at which the arch emerges?
- .alert[**Quasistable Density**]: Can we estimate the complete shape of the arch? 
]

---

# Methods

---

# Methods: Exact Solutions

### .tiny[Exact]

]

]

---

# Methods: Exact Solutions

### .tiny[Exact]

]

![:scale 75%](img/borked.jpg)

]

---

# Methods: Pair Approximation

### .tiny[Exact]

### .tiny[PA]

]

.right-column[
.smaller[
A continuous-time mean field theory directly relating the fraction of ones `$q_1$` to edge densities `$x_{00}$`, `$x_{01}$`, and `$x_{11}$`. Approximates triplets of nodes as sets of pairs (moment closure):
The approximate update in the fraction of disagreeing edges `$x_{01}$` is 
]

.tiny[
`$$\frac{dx_{01}}{dt} = \underbrace{x_{01}}_{\text{removed}} -  \overbrace{(1-\alpha) x_{01}}^\text{created by rewiring} + \underbrace{(1-\alpha)\left[\frac{x_{10}x_{00}}{q_0} + \frac{x_{11}x_{10}}{q_1} - \frac{x_{10}x_{01}}{q_0} - \frac{x_{01}x_{10}}{q_1} \right]}_{\text{created/destroyed by voting}}$$`
]

.smaller[
Solve to obtain an approximation for the arch....that doesn't match the data very well. =(
]
]

---

# Methods: Pair Approximation

### .tiny[Exact]

### .tiny[PA]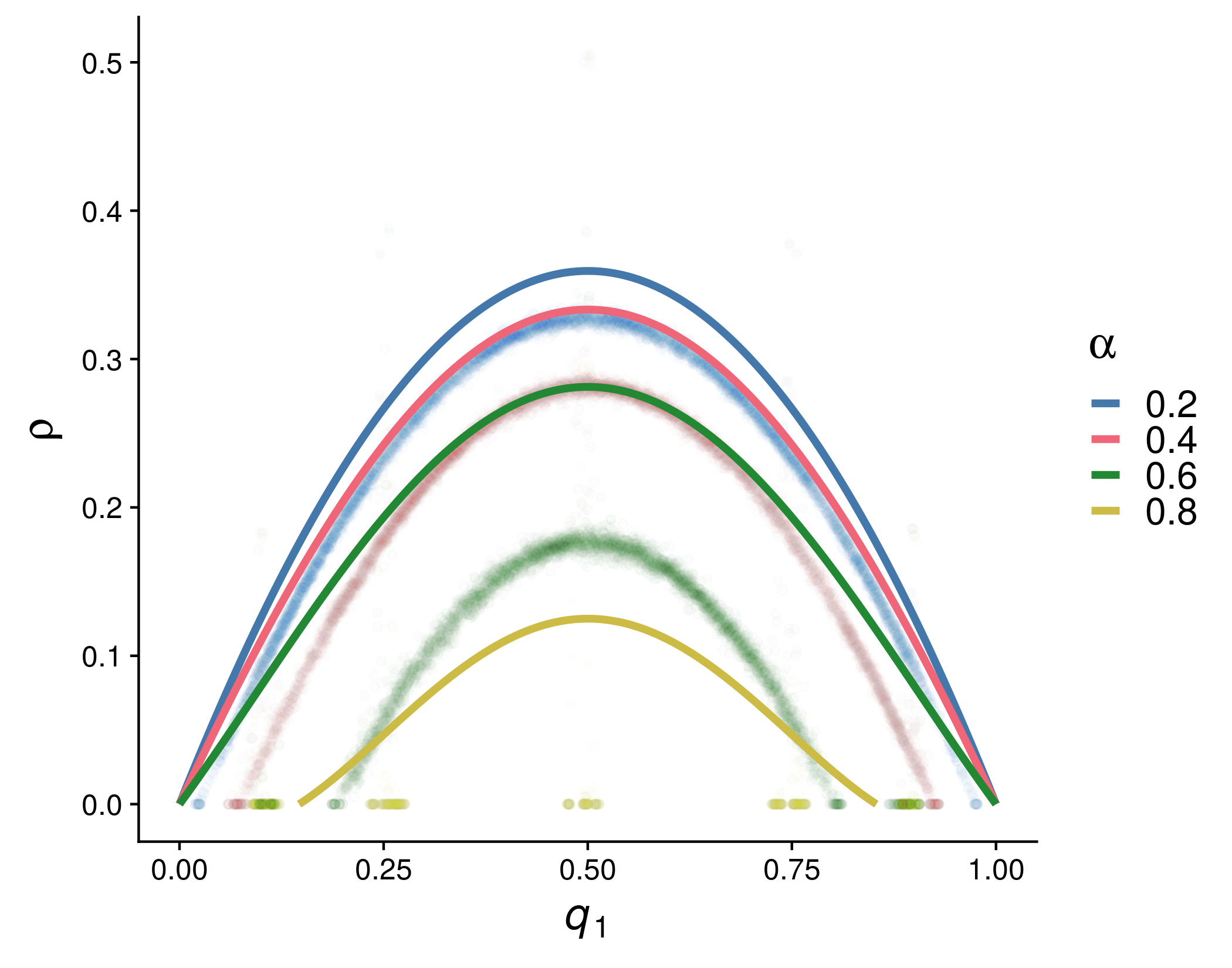

]

---

# Methods: Approximate Master Equations

### .tiny[Exact]

### .tiny[PA]

### .tiny[AMEs]
]

.right-column[
A continuous-time .alert[**compartmental**] approach: track node densities with `$j$` agreeing neighbors and `$k$` disagreeing neighbors, for each combination of `$k$` and `$j$`.

![:scale 60%](img/AME.png)

---

# Methods: Approximate Master Equations

### .tiny[Exact]

### .tiny[PA]

### .tiny[AMEs]
]

.right-column[
This works ok, but is not interpretable and scales poorly with mean degree. 
For mean degree 4, there are ~200 equations like the below.

![:scale 60%](img/AME.png)

---

# Methods: Bespoke

### .tiny[Exact]

### .tiny[PA]

### .tiny[AMEs]

### .tiny[.smaller[Bespoke]]
]

Literally anything else.

1). PDE approximations -- Silk et al., *New Journal of Physics* (2014)

2). Linearization near the emergence of the arch -- Bohme + Gross, *PRE* (2011)

3). .alert[**Discrete-time Markovian approximations**] -- Chodrow + Mucha, *SIAM J. Applied Math* (2020)
]

---
background-image: url('img/siam_journal.png')
background-size: contain

---

# Discrete-Time Markovian Approximations

`$$\underbrace{\mathbf{m}(t+1) - \mathbf{m}
(t)}_{\text{change in edge counts}} = \underbrace{\alpha\mathbb{E}[\mathbf{R}(\mathbf{x})]}_{\text{rewiring}} +\underbrace{(1-\alpha)\mathbb{E}[\mathbf{V}(\mathcal{G}(t))]}_{\text{voting}}$$`

We can approximate it by tracking each discordant edge (under some modeling assumptions).

Ugly bookkeeping, but easy computation.
]
.pull-right[

![:scale 60%](img/PJM.jpg)

Joint work with Peter Mucha, UNC
]

---
background-image: url('img/table.png')
background-size: contain

---
background-image: url('img/arch_approx.png')
background-size: contain

---

# Takeaways

Competing timescales of node and edge dynamics drive rich behavior even in simple systems.

It helps to treat these systems as truly discrete, rather than resort to continuous-time approximations.

This is a .alert[**great area**] for applied mathematicians, with lots of potential in evolutionary dynamics and theoretical ecology.

**The best work here is yet to come!**

---

background-color: #000000
background-image: url(img/boldly.jpg)
background-size: contain

---

# Thanks!

[philchodrow.com](https://www.philchodrow.com)

@philchodrow

MIT `$\rightarrow$` UCLA]
]

![:scale 73%](img/siam_journal.png)