Edge-Correlated Growing Hypergraphs

Conference on Network Science, Québec City | June 19th, 2024

Phil Chodrow
Department of Computer Science
Middlebury College

Hi everyone!

I’m Phil Chodrow. I’m an applied mathematician by training. These days my interests include:

• Network models + algorithms
• Dynamics on networks
• Data science for social justice
• Undergraduate pedagogy

Hi everyone!

I’m a new(ish) assistant professor of computer science at Middlebury College in Middlebury, Vermont.

Middlebury is a small primarily-undergraduate institution (PUI) in Vermont, USA.

Hypergraphs

A hypergraph is a generalization of a graph in which edges may contain an arbitrary number of nodes.

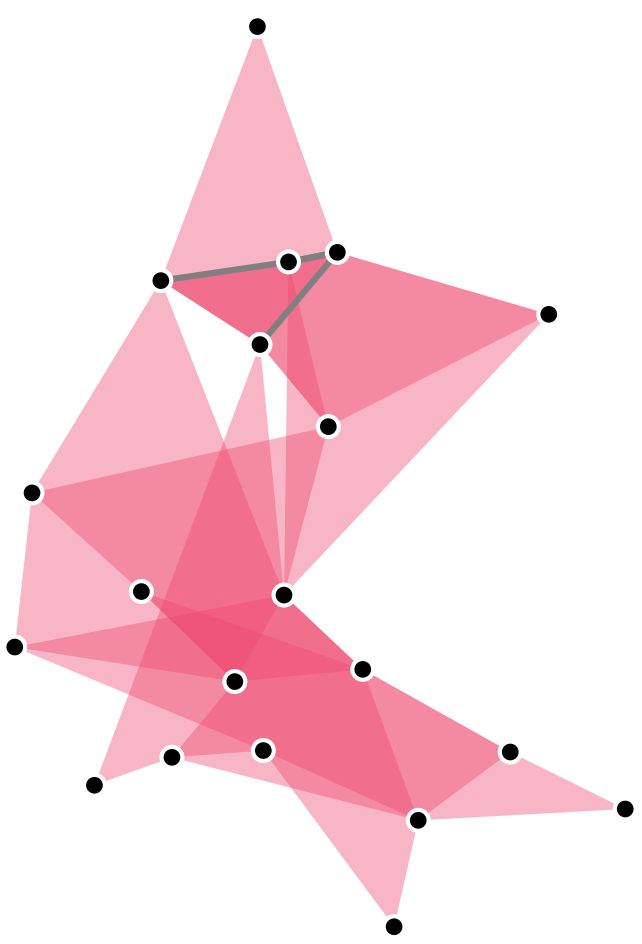
XGI let’s gooooo

What’s special about hypergraphs?

What can we observe or learn in hypergraph structure that we couldn’t observe or learn in a dyadic graph?

One answer for today: 2-edge motifs.

XGI let’s gooooo

Motifs in graphs

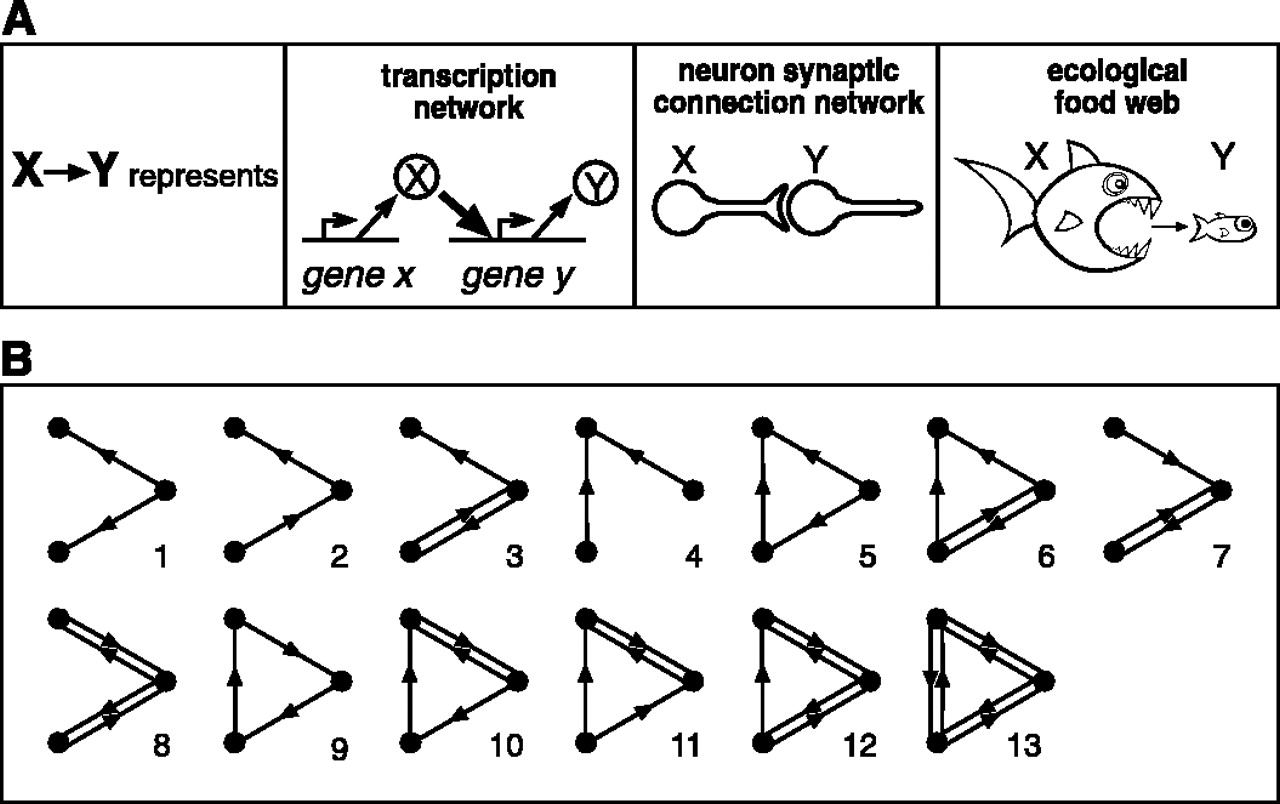
Milo et al. (2002). Network Motifs: Simple Building Blocks of Complex Networks. Science

Motifs in graphs

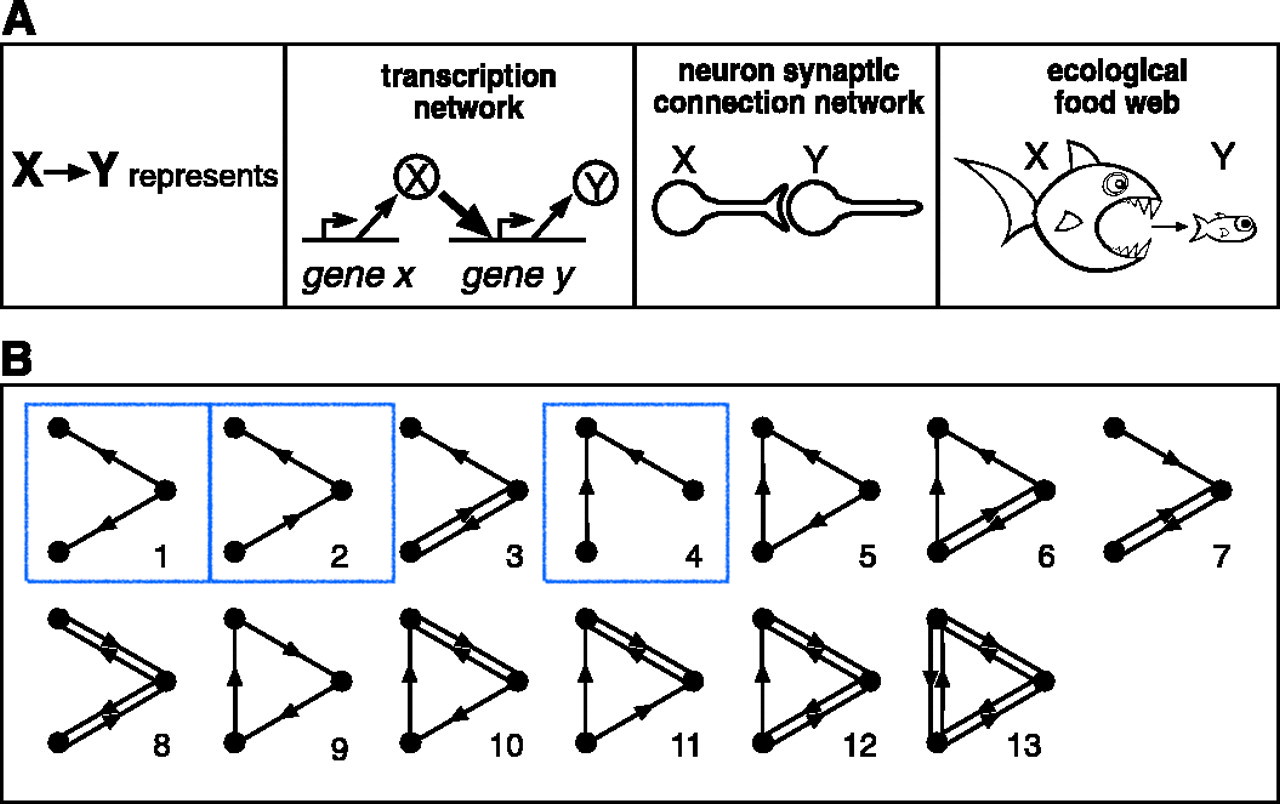
Milo et al. (2002). Network Motifs: Simple Building Blocks of Complex Networks. Science

2-edge motifs in undirected graphs

2-edge motifs in hypergraphs

Claim: What’s special about the structure of hypergraphs is that they have diverse, undirected, two-edge motifs: intersections.

How common are large intersections in empirical hypergraphs?

For the remainder of this talk, we’ll consider hypergraphs in which each edge has a discrete time-index: \(e_0, \; e_1, \ldots, e_t,\ldots\).

One way to measure the prevalence of intersections is to define an temporal intersection profile: the probability of an intersection of size \(k\) when picking two uniformly random edges.

\[r_k^{(t)} \triangleq \eta_t(\lvert e\cap f \rvert = k)\;,\]

where \(\eta_t\) is the empirical law of the hypergraph \(H^{(t)}\) containing only edges with indices up to \(t\) and \(e\), \(f\) are sampled uniformly from \(H^{(t)}\).

Sometimes there is a natural indexing of edges via temporal timestamps; other times we need to assign indices arbitrarily.

Intersections

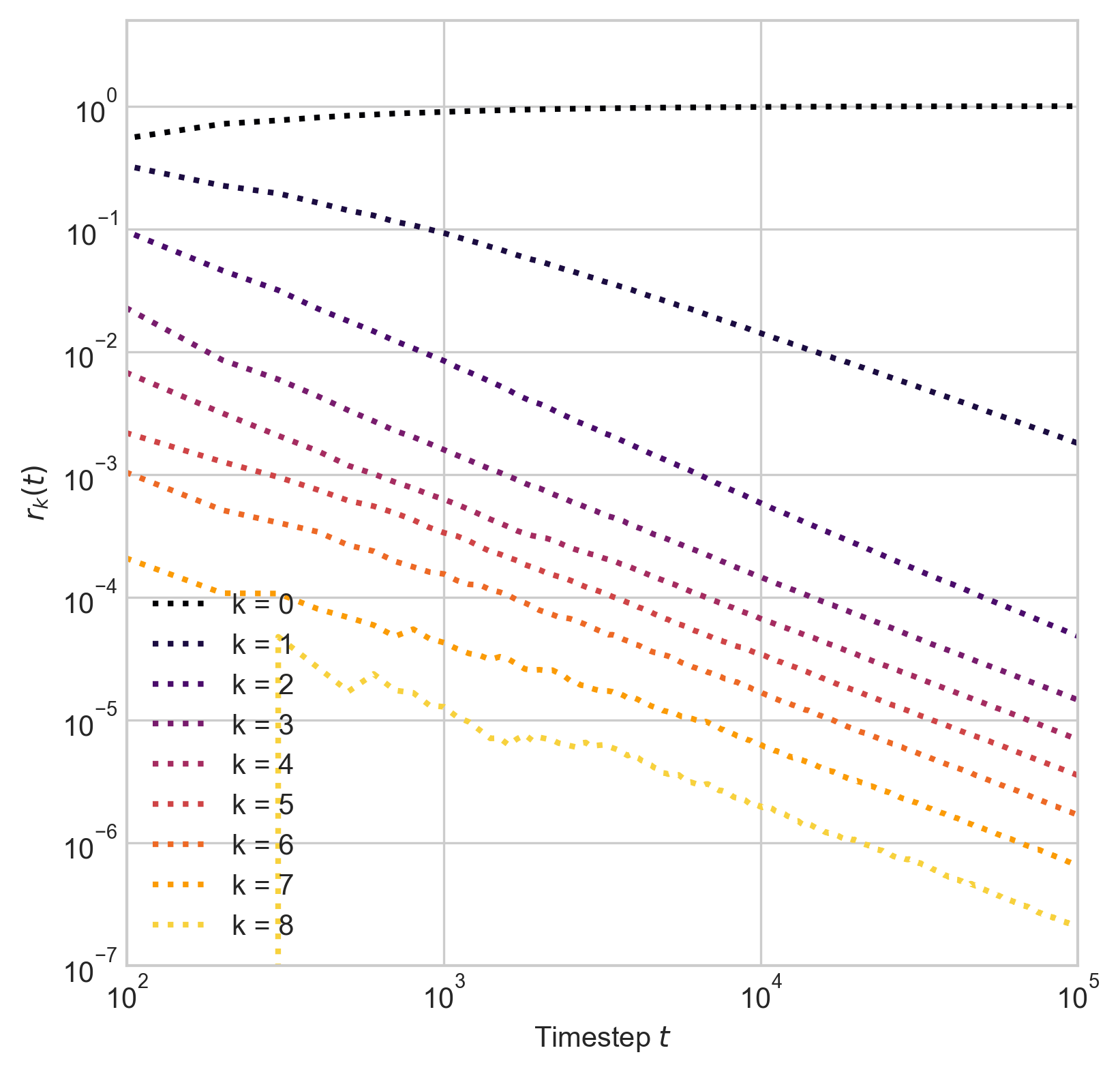
In empirical temporal hypergraphs, the intersection profile \(r_k^{(t)}\) often decays at rates close to \(t^{-1}\) or \(t^{-2}\), regardless of \(k\).

This is interesting because an growing Erdős–Rényi hypergraph would have \(k\)-intersections which decay at rate \(t^{-k}\).

Benson, Abebe, Schaub, and Kleinberg (2018). Simplicial closure and higher-order link prediction. PNAS

Chodrow (2020). Configuration models of random hypergraphs. JCN

Landry, Young, and Eikmeier (2023). The simpliciality of higher-order networks. EPJ Data Sci.

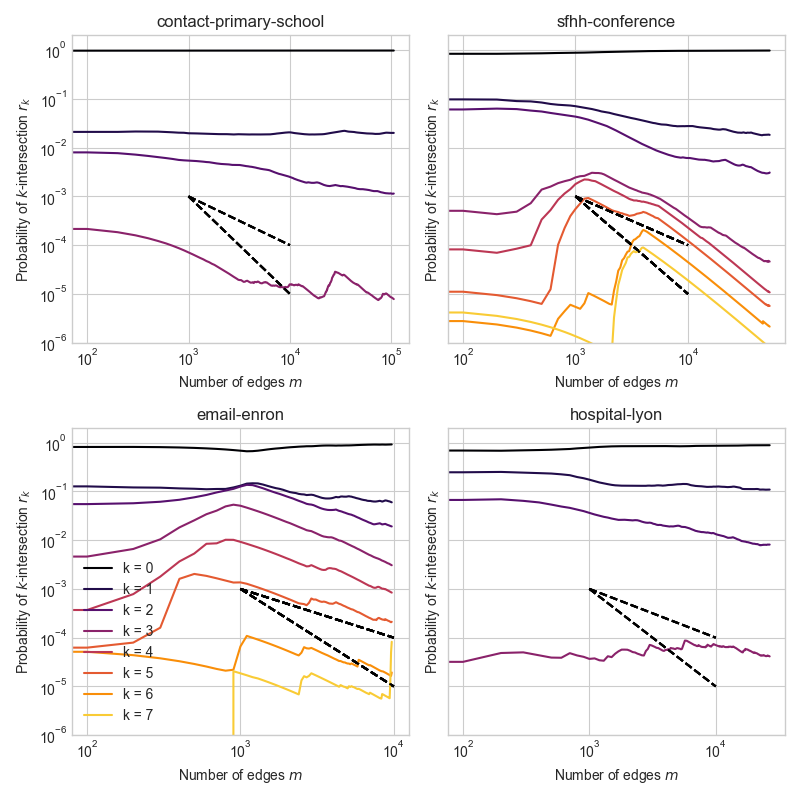
Dashed lines give slope of \(t^{-1}\) and \(t^{-2}\) decay.

Ongoing work with…

Xie He
Mathematics
Dartmouth College

Peter Mucha
Mathematics
Dartmouth College

Mechanistic, interpretable, learnable models of growing hypergraphs.

Motivation: New edges are usually pretty similar to some older edges.

Benson, Kumar, and Tomkins (2018). Sequences of Sets. KDD

Benson, Abebe, Schaub, and Kleinberg (2018). Simplicial closure and higher-order link prediction. PNAS

In each timestep…

Select a random edge

Select random nodes from edge

Add nodes from hypergraph

Add novel nodes

Form edge

Repeat

Repeat

Formally

In each timestep \(t\):

• Start with an empty edge \(f = \emptyset\).
• Select an edge \(e \in H\).
• Accept each node from \(e\) into \(f\) with probability \(\alpha\) (condition on at least one).
  
• Add \(X\) novel nodes.
• Add \(Y\) nodes from \(H \setminus e\).

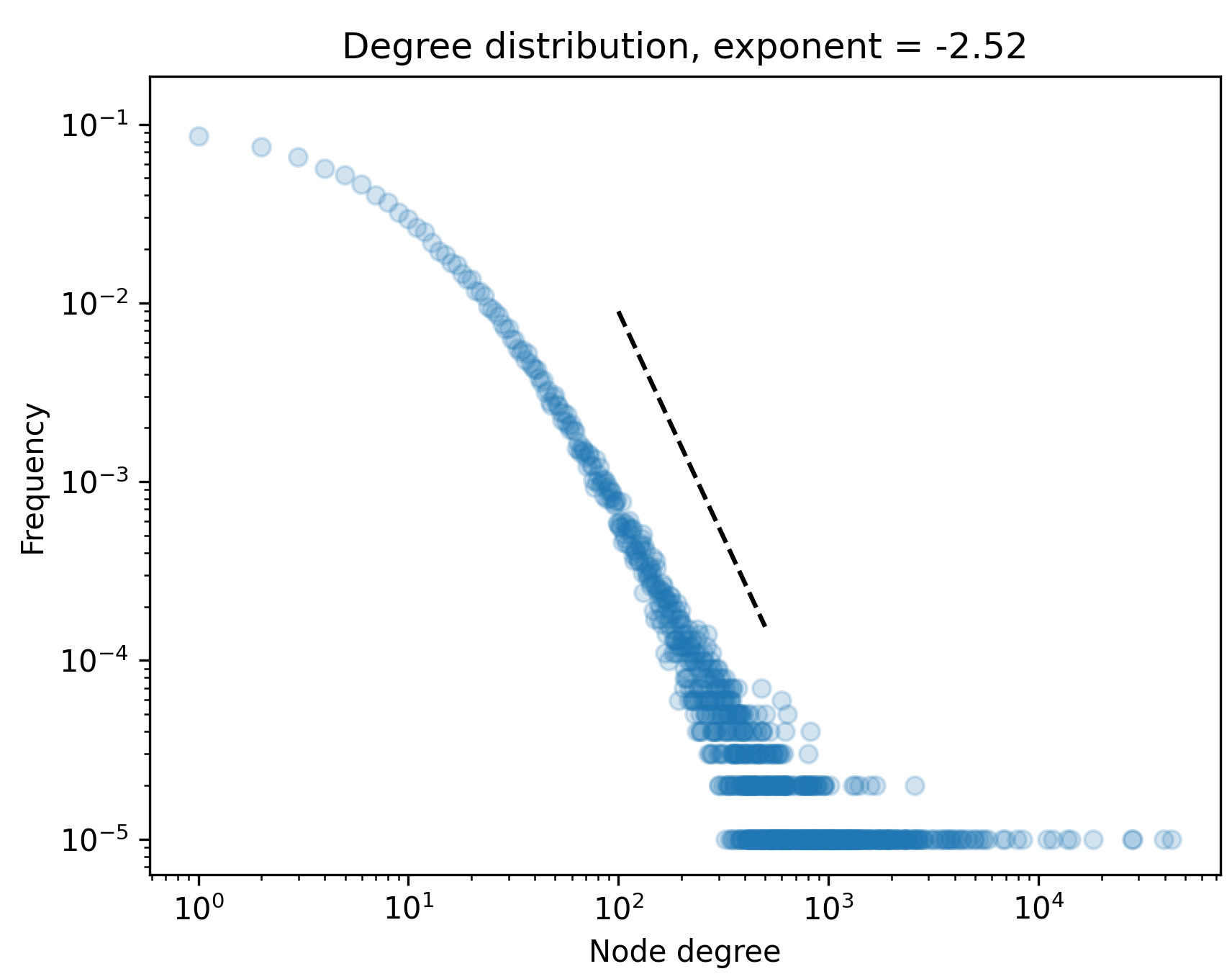
Power-law heavy-tailed degree distribution

Proposition (He, Chodrow, Mucha ’24): As \(t\) grows large, the degrees of \(H_t\) converge in distribution to a power law with exponent
\[ p = 1 + \frac{1-\alpha +\mathbb{E}[X] +\mathbb{E}[Y] }{1-\alpha(1 + \mathbb{E}[X] + \mathbb{E}[Y] )}\;. \]

Reminders:

• \(\alpha\): retention rate of nodes in sampled edge.
• \(X\): number of novel nodes added to edge.
• \(Y\): number of nodes from \(H\) added to edge.

Some connections to preferential attachment hypergraphs:

Avin, Lotker, Nahum, and Peleg (2019). Random preferential attachment hypergraph. ASONAM

Roh and Goh (2023) Growing hypergraphs with preferential linking. J. Korean Phys. Soc.

Edge intersections

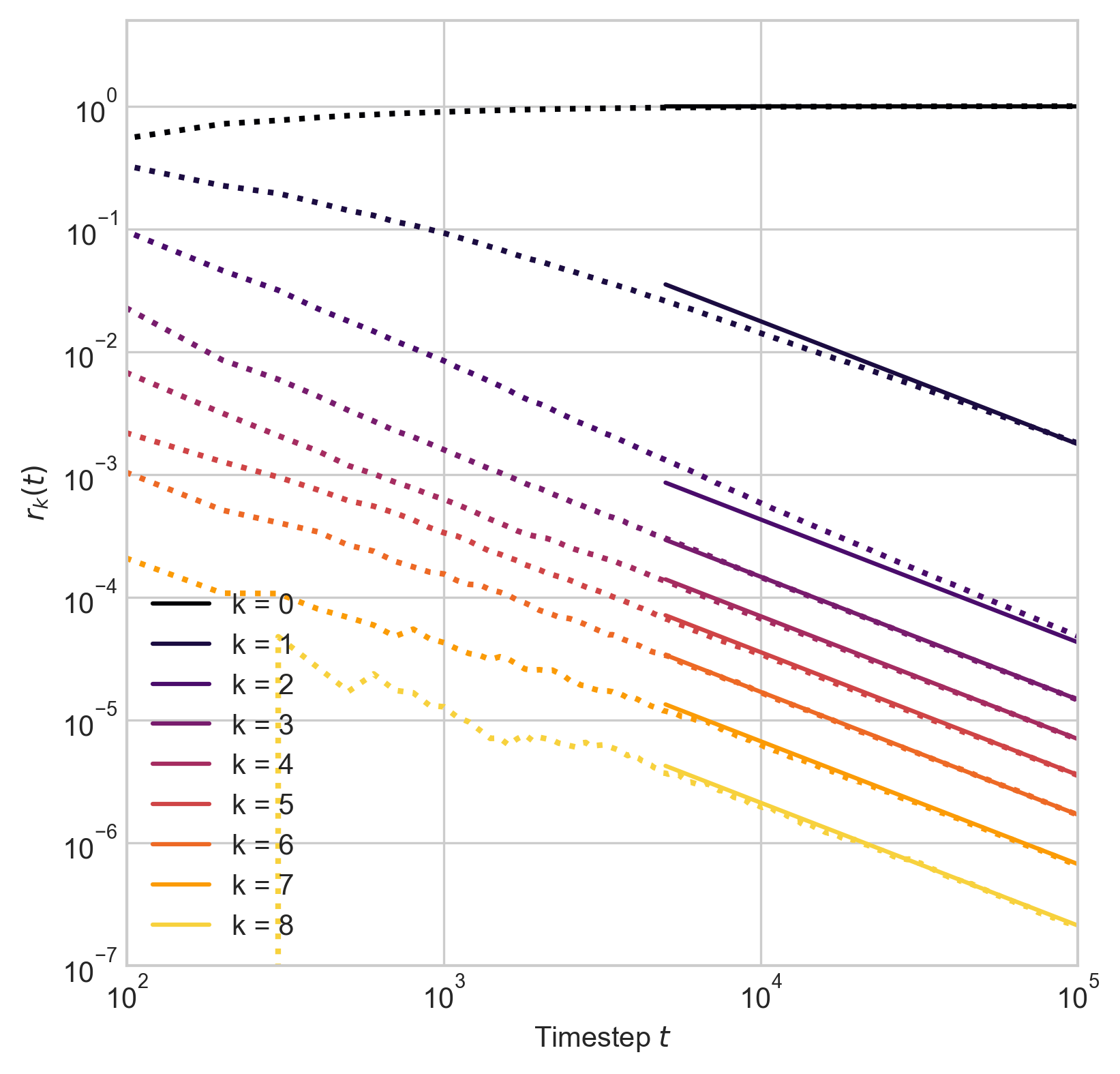
Proposition (He, Chodrow, Mucha ’24): There exist constants \(q_k\) such that, as \(t\rightarrow \infty\),

\[ \begin{aligned} r_{k}(t) \simeq \begin{cases} q_k & \quad \text{if } k \leq k_0\\ t^{-1} q_k &\quad \mathrm{otherwise}\;. \end{cases} \end{aligned} \]

Here, \(q_k = \sum_{ij} q_{ijk}\) and \(\{q_{ijk}\}\) solve the system

\[ q_{ijk} = \begin{cases} \frac{1}{2}\sum_{\ell} \left(q_{\ell j 0} \alpha_{i0|\ell j0} + q_{j \ell 0} \alpha_{i0|j\ell 0}\right) & \quad k = 0\\ \frac{1}{2}\beta_{ik|j} \sum_{\ell} (q_{\ell j0} + q_{j\ell 0}) + \frac{1}{2}\sum_{\ell, h\geq k} \left(q_{\ell j h} \alpha_{ik|\ell jh} + q_{j \ell h} \alpha_{ik|j\ell h}\right) &\quad k \geq 1\;, \end{cases} \]

where \(\alpha_{ik|\ell jh}\) and \(\beta_{ik|j}\) are constants determined by the model parameters.

These come out of linearized compartmental equations.

Edge intersections

Proposition: There exist constants \(q_k\) such that, as \(t\rightarrow \infty\),

\[ \begin{aligned} r_{k}(t) \simeq \begin{cases} q_k & \quad \text{if } k \leq k_0\\ t^{-1} q_k &\quad \mathrm{otherwise}\;. \end{cases} \end{aligned} \]

Learning from data

Aim: given the sequence of edges \(\{e_t\}\), estimate:

• \(\alpha\), the edge retention rate.
• \(p_X\), the distribution of the number of novel nodes added to each edge.
• \(p_Y\), distribution of the number of pre-existing nodes added to each edge.

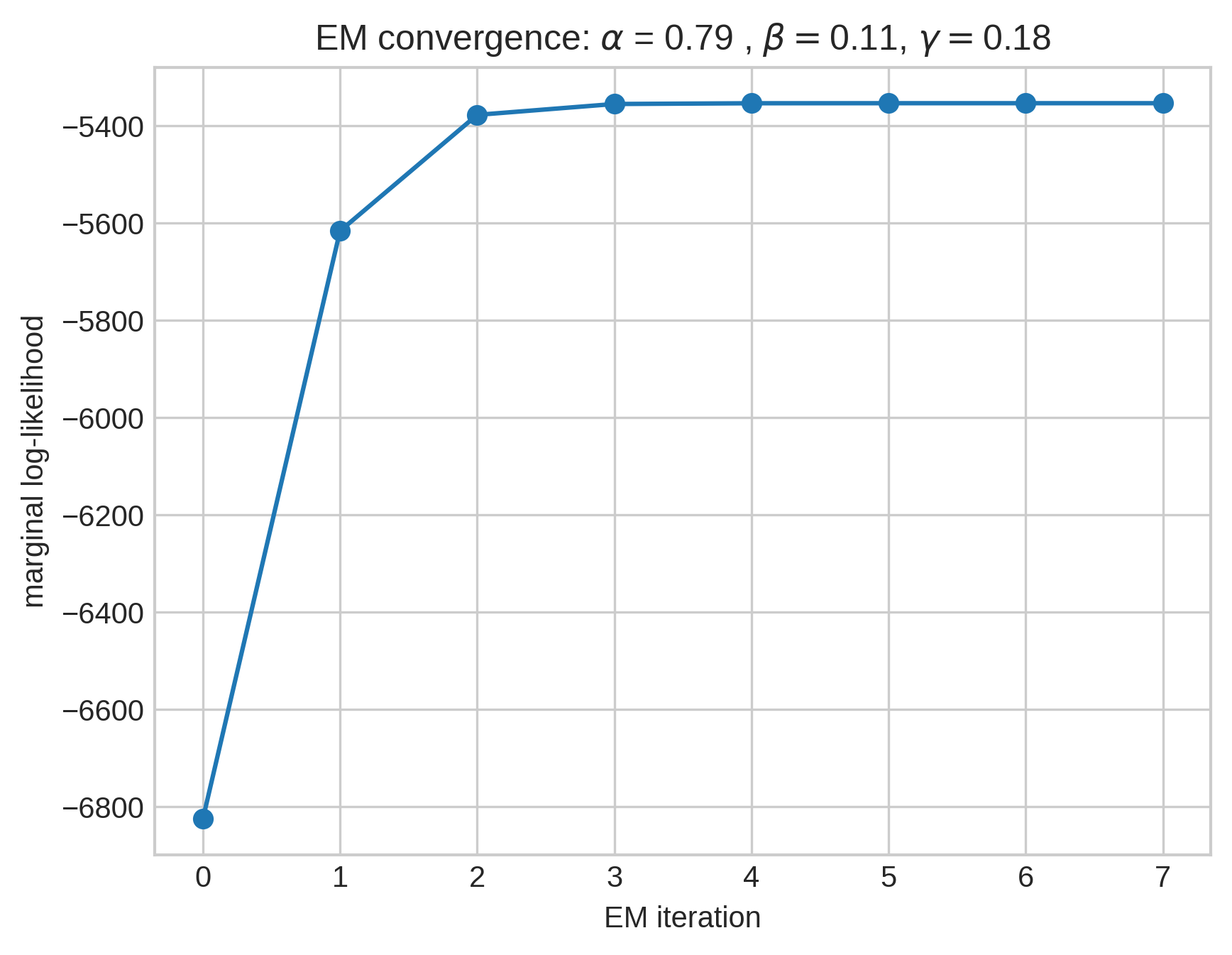
Expectation maximization:

1. For each edge \(e_t\), form a belief about which prior edge \(f \in H_{t-1}\) \(e_t\) was sampled from.
2. Maximize the expected complete log-likelihood with respect to \(\alpha\), \(p_X\), and \(p_Y\) under this belief.

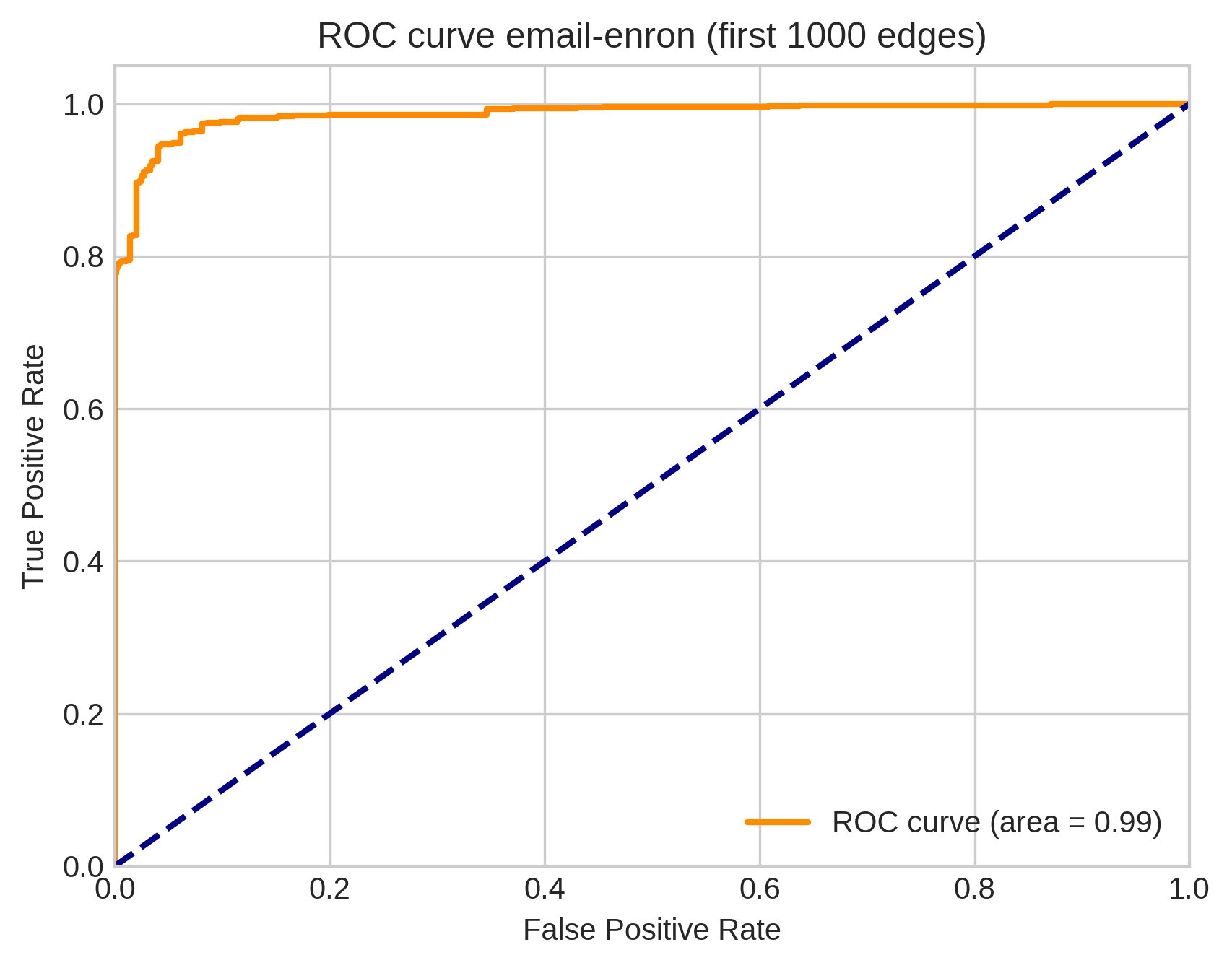
Simple models can be predictive!

We computed AUC scores for a link prediction task in which our model learns parameters on 20% training data from three metabolic and organic reaction data sets with edges up to size 5. We compared these against previously-reported AUC scores on the same task for two dedicated neural network hypergraph link prediction algorithms.

Yadati et al. (2020) NHP: Neural Hypergraph Link Prediction. CIKM

Yang et al. (2023) LHP: Logical hypergraph link prediction. Expert Systems with Applications

	\(n\)	\(m\)	Our model	NHP AUC	LHP AUC
iAF1260b	1,668	2,084	0.643	0.582	0.639
iJO1366	1,805	2,253	0.769	0.599	0.638
USPTO	16,293	11,433	0.550	0.662	0.733

We are competitive with neural networks using an 11-parameter model!

Summing up

Hypergraphs are locally distinct from graphs in that they have interesting two-edge motifs (intersections).

Learnable, mechanistic models of hypergraph formation allow us to both model this phenomenon and achieve competitive performance on link prediction problems.

arXiv coming soon 😬😬😬

Thanks everyone!

Xie He
Dartmouth College

Peter Mucha
Dartmouth College