Math Models of Hierarchy: Dominance, Dynamics, and Data

Smith College | April 6th, 2023

Dr. Phil Chodrow
Department of Computer Science
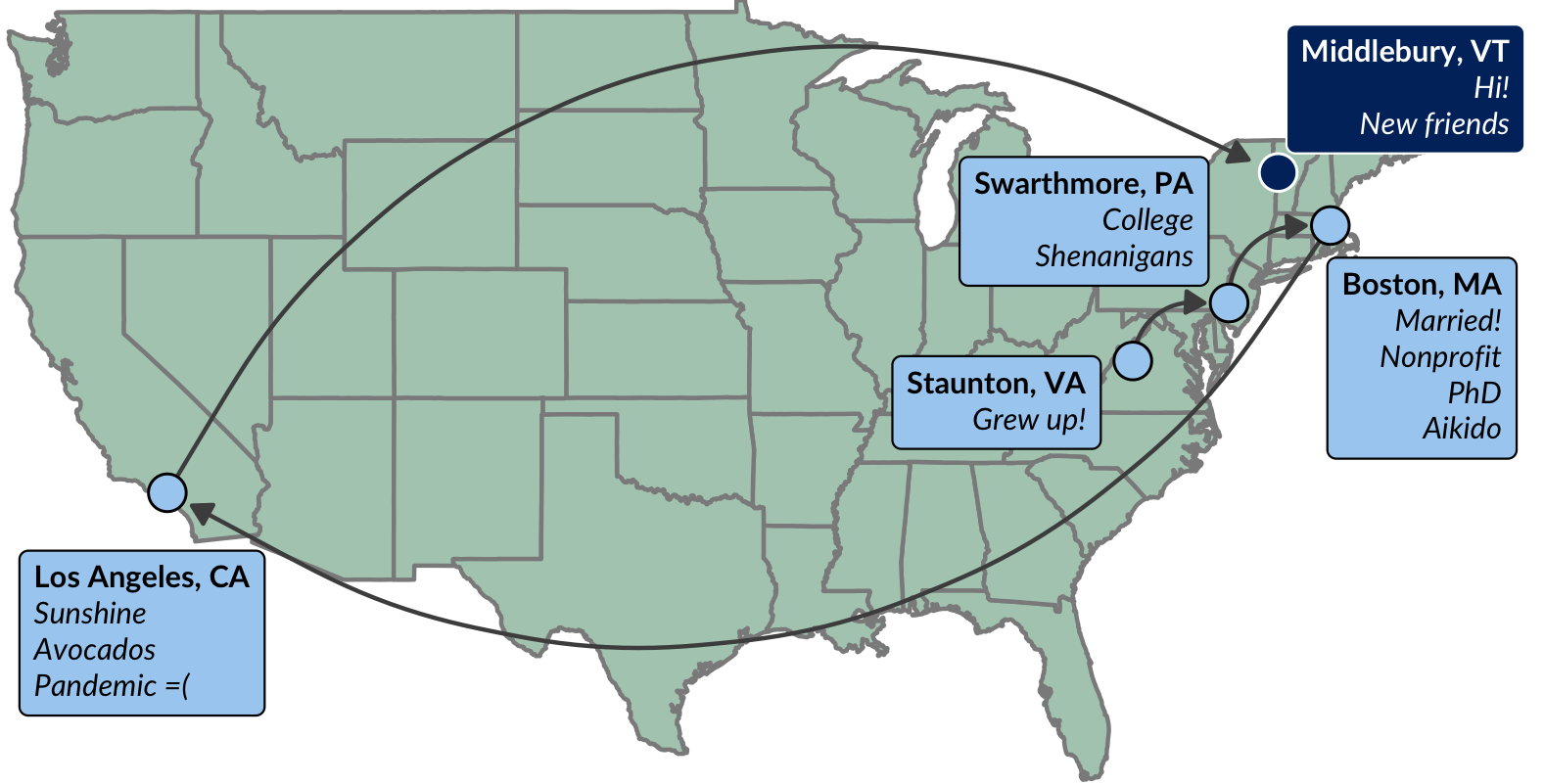
Middlebury College

Hi! I’m Phil.

I am an
applied mathematician
and
STEM educator.

I like…

• Mathematics of complex systems
• Network science
• Ethics and technology
• Traditional martial arts
• Tea
• Star Trek: Deep Space 9
• Effective pedagogy

I’m a new professor in the department of computer science at Middlebury College in Middlebury, Vermont.

I teach machine learning, discrete math, introductory computing, and network science.

My Journey

$$

$$

This is a talk about hierarchy

the classification of a group of people according to ability or to economic, social, or professional standing

a graded or ranked series

- Merriam Webster

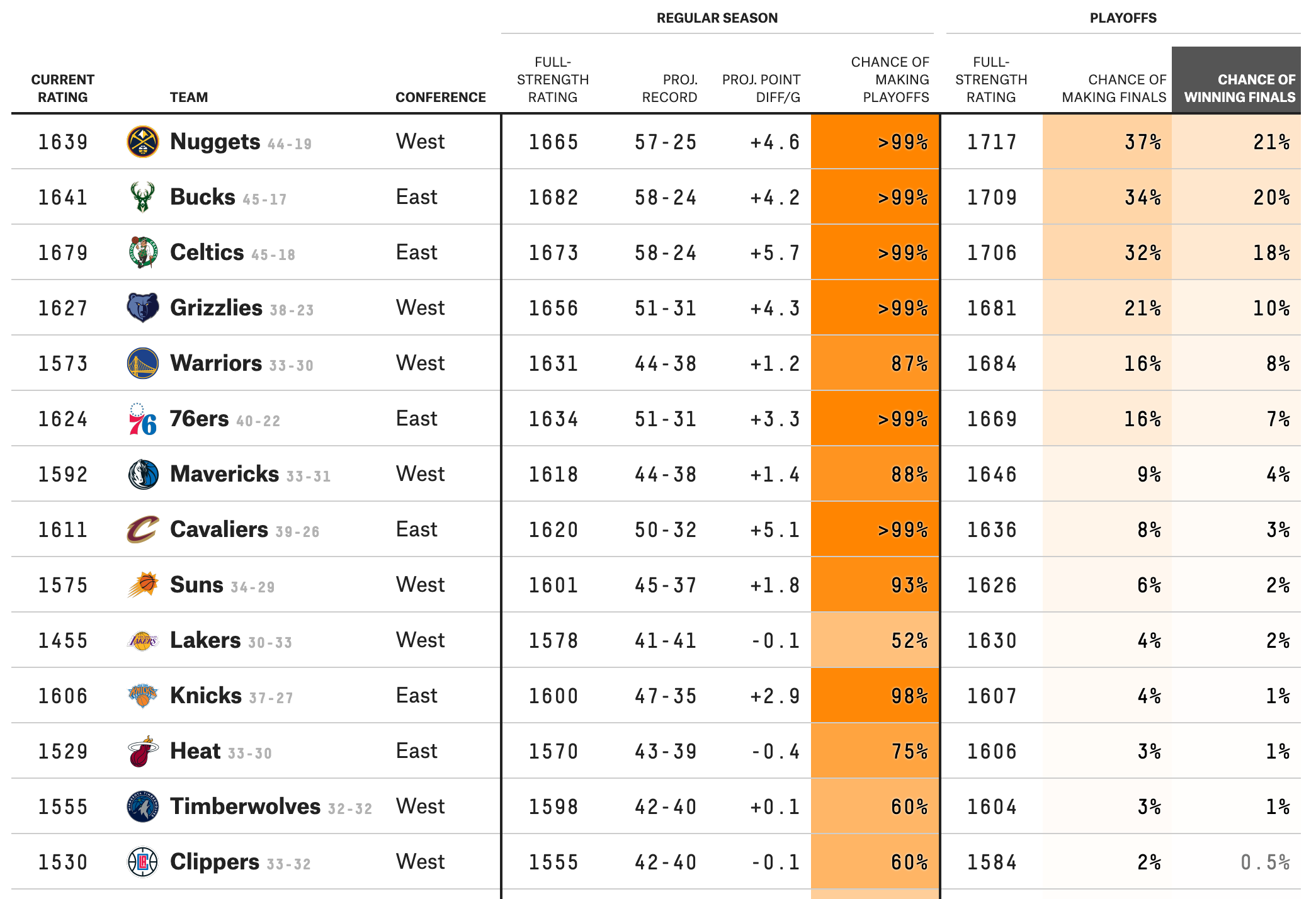
Examples of hierarchies

Standings in competitions

Rankings of colleges, PhD programs, etc.

Popularity

Dominance in animal societies

Some hierarchies are helpful

Others are Fake and Toxic ttttttt ttttttt ttttt

1. Can hierarchies sustain themselves on the basis of nothing but prestige?

2. Can we infer how agents interact with hierarchies from data?

3. What makes science joyful (for me)?

Collaboration Origin Story

Complex Networks Winter Workshop 2019

18 Months Later…

Mari Kawakatsu
UPenn and Princeton
Nicole Eikmeier
Grinnell
Dan Larremore
CU Boulder

A model of prestige-based hierarchy

We have \(n\) agents.

These agents can “endorse” each other.

When agent \(i\) endorses agent \(j\), we interpret this as agent \(i\) signalling that agent \(j\) is of high prestige.

“Endorsements:”

• Player \(i\) loses a match to player \(j\).
• University \(i\) hires a scholar trained at university \(j\).
• Individual \(i\) claims that \(j\) is their friend.
• …

A model of prestige-based hierarchy

A state of the model is a matrix \(\mathbf{A}^{(t)} \in \mathbb{R}^{n\times n}\) of endorsements.

\(a_{ij}^{(t)}\) is the weighted number times that \(i\) has endorsed \(j\).

At each timestep, we update \(\mathbf{A}^{(t)}\): \[ \mathbf{A}^{(t+1)} = \lambda \mathbf{A}^{(t)} + (1-\lambda) \Delta^{(t)} \] where \(\Delta^{(t)}\) is the matrix of new endorsements.

\(\lambda\) acts as the rate of exponentially decaying system memory.

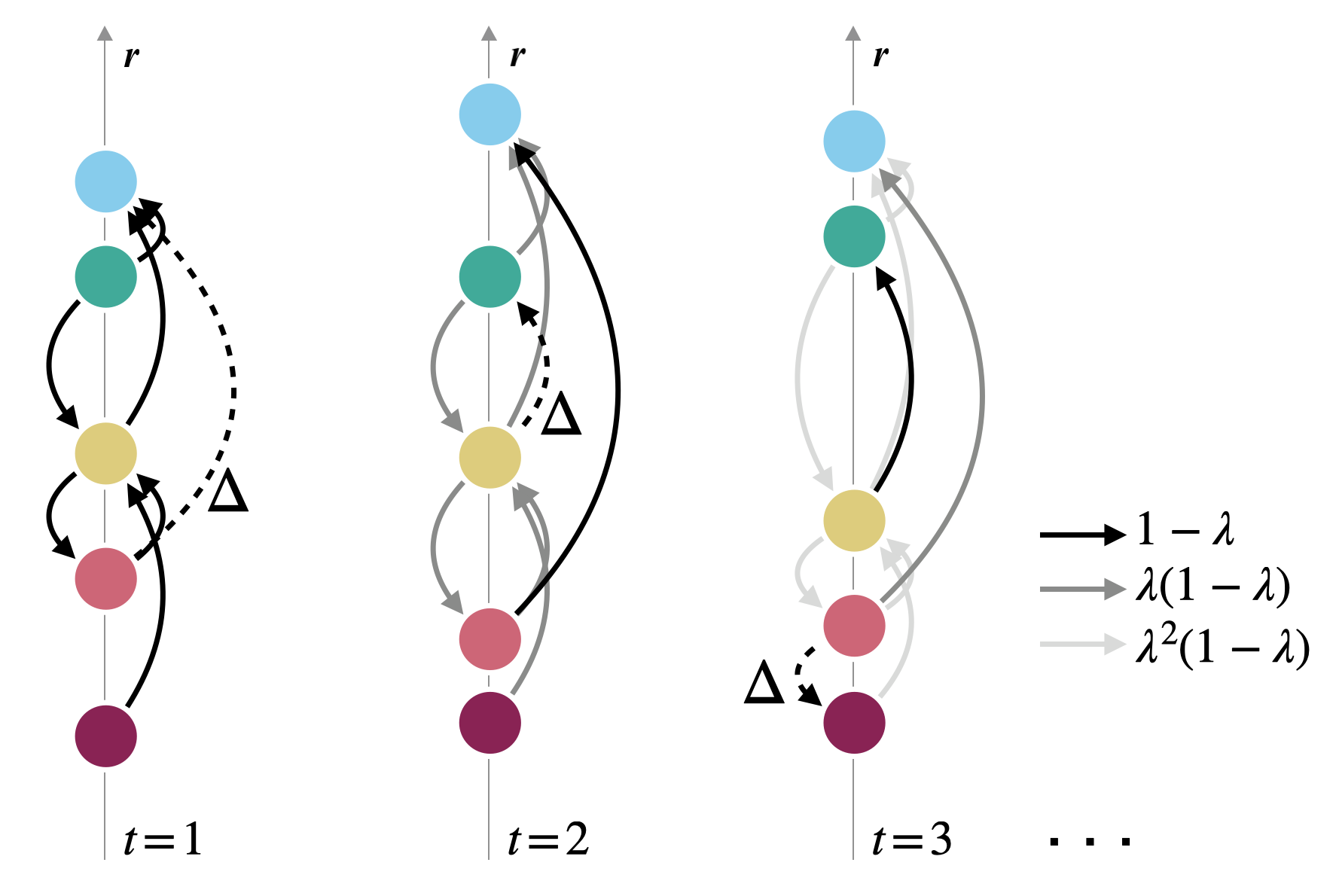
New Endorsements

Agents endorse other agents that they perceive as being of high prestige.

Prestige is measured by a score function \(\sigma: \mathbf{A}^{(t)} \mapsto \mathbf{r}^{(t)} \in \mathbb{R}^n\).

Each agent \(i\) computes a utility of endorsing agent \(j\) in terms of the score vector \(\mathbf{r}^{(t)}\). Our utility is: \[ u_{ij}(\mathbf{r}) = \beta_1 s_j + \beta_2 (r_i - r_j)^2. \]

Agent \(i\) endorses \(j\) at time \(t+1\) with probability \[ p_{ij}^{(t)} = \frac{e^{u_{ij}(\mathbf{r}^{(t)})}}{\sum_j e^{u_{ij}(\mathbf{r}^{(t)})}} \]

All new endorsements get collected into update matrix \(\Delta^{(t)}\). Then we do our main update: \[ \mathbf{A}^{(t+1)} = \lambda \mathbf{A}^{(t)} + (1-\lambda) \Delta^{(t)}\;. \]

We allow \(m\in \mathbb{Z}\) endorsements per round.

New Endorsements

Agents endorse other agents that they perceive as being of high prestige.

Prestige is measured by a score function \(\sigma: \mathbf{A}^{(t)} \mapsto \mathbf{r}^{(t)} \in \mathbb{R}^n\).

Each agent \(i\) computes a utility of endorsing agent \(j\) in terms of the score vector \(\mathbf{r}^{(t)}\). Our utility is: \[ u_{ij}(\mathbf{r}) = \color{#FFD447}{\beta_1} s_j + \color{#59C9A5}{\beta_2} (r_i - r_j)^2. \]

Agent \(i\) endorses \(j\) at time \(t+1\) with probability \[ p_{ij}^{(t)} = \frac{e^{u_{ij}(\mathbf{r}^{(t)})}}{\sum_j e^{u_{ij}(\mathbf{r}^{(t)})}} \]

We allow \(m\in \mathbb{Z}\) endorsements per round.

\(\beta_1\) encodes a preference to endorse high-prestige agents. Higher value: more likely for endorsements to concentrate at the top.

\(\beta_2\) encodes a preference to endorse agents that are similar in prestige to you. Negative value: more likely for endorsements to “travel” only a little way up the hierarchy.

The score function \(\sigma\) maps the matrix of endorsements \(\mathbf{A} \in \mathbb{R}^{n\times n}\) to a vector of scores \(\mathbf{s} \in \mathbb{R}^n\). There are lots of choices!

In-Degree

\(s_i\) is the number of times that agent \(i\) h as been endorsed: \(\mathbf{r} = \mathbb{1}^T\mathbf{A}\)

PageRank

\(\mathbf{r}\) is the eigenvector with eigenvalue \(1\) of the matrix \(\mathbf{P}\) with entries \[ p_{ij} = (1-\alpha)\frac{a_{ij}}{d_i} + \frac{\alpha}{n} \]

SpringRank

\(\mathbf{r}\) is the unique solution of the system \[ \left[\mathbf{L} - \alpha \mathbf{I}\right]\mathbf{r} = \mathbf{D}^{\mathrm{in}} - \mathbf{D}^{\mathrm{out}} \]

\(\mathbf{D}^{\mathrm{in}} = \mathrm{diag}(\mathbb{1}^T\mathbf{A})\) and \(\mathbf{D}^{\mathrm{out}} = \mathrm{diag}(\mathbf{A}\mathbb{1})\)

1. Can hierarchies sustain themselves on the basis of nothing but prestige?

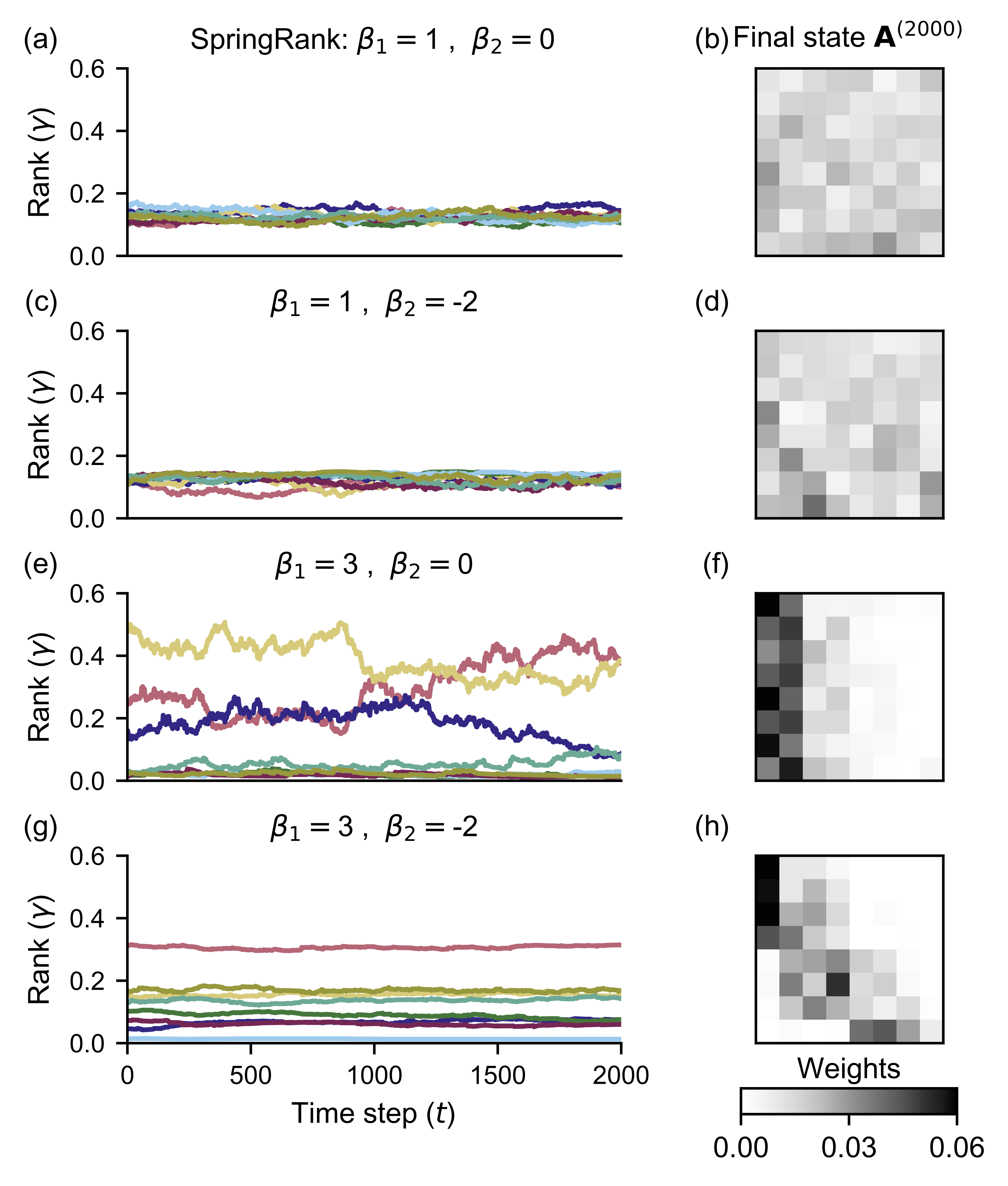
Yes, and there is a phase transition (qualitative behavior shift) depending on the parameters.

Model do?

\(\beta_1\) preference for prestige.

• \(\beta_1\) small: fluctuating egalitarianism.
• \(\beta_1\) large: emergence of time-varying hierarchies.

\(\beta_2\) preference for proximity.

• \(\beta_2 < 0\): stabilization of hierarchical ranks.

Two math problems

Dynamics: can we mathematically characterize when we observe egalitarianism and when we observe hierarchy in terms of the score function, \(\beta_1\), and \(\beta_2\)?

Data science: can we determine which score functions and parameters best describe the behavior of real systems?

Theorem: KCEL ’21

Consider the deterministic function \[\mathbf{f}(\mathbf{r}, \mathbf{A}) = \lim_{\lambda \rightarrow 1} \frac{\mathbb{E}[\mathbf{r}|\mathbf{A}] - \mathbf{r}}{1 - \lambda}\;.\]

This function has an egalitarian fixed point, where all ranks are the same. This point fixed point is linearly stable iff \(\beta_1 < \beta_1^c\):

\[\beta_1^c = \begin{cases} 2\sqrt{\frac{n}{m}} &\quad \text{Root-Degree} \\ 1/\alpha_p &\quad \text{PageRank} \\ 2 + \alpha_s\frac{n}{m} &\quad \text{SpringRank}. \end{cases}\]

Theorem: KCEL ’21

Consider the deterministic function \[\mathbf{f}(\mathbf{r}, \mathbf{A}) = \lim_{\lambda \rightarrow 1} \frac{\mathbb{E}[\mathbf{r}|\mathbf{A}] - \mathbf{r}}{1 - \lambda}\;.\]

This function has an egalitarian fixed point, where all ranks are the same. This point fixed point is linearly stable iff \(\beta_1 < \beta_1^c\):

\[\beta_1^c = \begin{cases} 2\sqrt{\frac{n}{m}} &\quad \text{Root-Degree} \\ 1/\alpha_p &\quad \text{PageRank} \\ 2 + \alpha_s\frac{n}{m} &\quad \text{SpringRank}. \end{cases}\]

Linear Stability

Heuristically, a fixed point \(\mathbf{x}_0\) of some dynamics is stable if, when you perturb the the system to some nearby point, it eventually comes back to \(\mathbf{x}_0\).

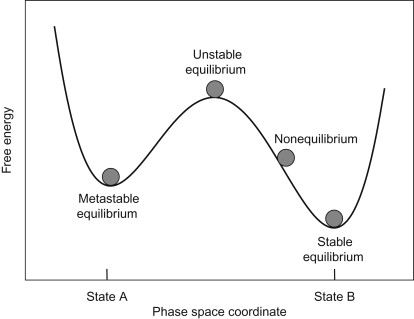Image credit: Desmond Winterborne

Theorem: KCEL ’21

Consider the deterministic function \[\mathbf{f}(\mathbf{r}, \mathbf{A}) = \lim_{\lambda \rightarrow 1} \frac{\mathbb{E}[\mathbf{r}|\mathbf{A}] - \mathbf{r}}{1 - \lambda}\;.\]

This function has an egalitarian fixed point, where all ranks are the same. This point fixed point is linearly stable iff \(\beta_1 < \beta_1^c\):

\[\beta_1^c = \begin{cases} 2\sqrt{\frac{n}{m}} &\quad \text{Root-Degree} \\ 1/\alpha_p &\quad \text{PageRank} \\ 2 + \alpha_s\frac{n}{m} &\quad \text{SpringRank}. \end{cases}\]

Linear Stability

Here, stability of the egalitarian fixed point of \(\mathbf{f}\) is governed by the Jacobian matrix of partial derivatives:

\[\mathbf{J} = \left[\begin{matrix}\frac{\partial f_1}{\partial r_1} & \frac{\partial f_1}{\partial r_2} & \cdots & \frac{\partial f_1}{\partial r_n} \\ \frac{\partial f_2}{\partial r_1} & \frac{\partial f_2}{\partial r_2} & \cdots & \frac{\partial f_2}{\partial r_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial r_1} & \frac{\partial f_n}{\partial r_2} & \cdots & \frac{\partial f_n}{\partial r_n} \end{matrix}\right]\]

Fixed point is linearly stable if \(\mathbf{J}\) only has eigenvalues with negative real part.

So, we can assess the stability of egalitarianism in this system with calculus + linear algebra.

Theorem: KCEL ’21

Consider the deterministic function \[\mathbf{f}(\mathbf{r}, \mathbf{A}) = \lim_{\lambda \rightarrow 1} \frac{\mathbb{E}[\mathbf{r}|\mathbf{A}] - \mathbf{r}}{1 - \lambda}\;.\]

This function has an egalitarian fixed point, where all ranks are the same. This point fixed point is linearly stable iff \(\beta_1 < \beta_1^c\):

\[\beta_1^c = \begin{cases} 2\sqrt{\frac{n}{m}} &\quad \text{Root-Degree} \\ 1/\alpha_p &\quad \text{PageRank} \\ 2 + \alpha_s\frac{n}{m} &\quad \text{SpringRank}. \end{cases}\]

Theorem: KCEL ’21

Consider the deterministic function \[\mathbf{f}(\mathbf{r}, \mathbf{A}) = \lim_{\lambda \rightarrow 1} \frac{\mathbb{E}[\mathbf{r}|\mathbf{A}] - \mathbf{r}}{1 - \lambda}\;.\]

This function has an egalitarian fixed point, where all ranks are the same. This point fixed point is linearly stable iff \(\beta_1 < \beta_1^c\):

\[\beta_1^c = \begin{cases} 2\sqrt{\frac{n}{m}} &\quad \text{Root-Degree} \\ 1/\alpha_p &\quad \text{PageRank} \\ 2 + \alpha_s\frac{n}{m} &\quad \text{SpringRank}. \end{cases}\]

Theorem: KCEL ’21

Consider the deterministic function \[\mathbf{f}(\mathbf{r}, \mathbf{A}) = \lim_{\lambda \rightarrow 1} \frac{\mathbb{E}[\mathbf{r}|\mathbf{A}] - \mathbf{r}}{1 - \lambda}\;.\]

This function has an egalitarian fixed point, where all ranks are the same. This point fixed point is linearly stable iff \(\beta_1 < \beta_1^c\):

\[\beta_1^c = \begin{cases} 2\sqrt{\frac{n}{m}} &\quad \text{Root-Degree} \\ 1/\alpha_p &\quad \text{PageRank} \\ 2 + \alpha_s\frac{n}{m} &\quad \text{SpringRank}. \end{cases}\]

Learnings

1. The stability of egalitarianism depends on the prestige preference \(\beta_1\) but not on the proximity preference \(\beta_2\).
2. The stability of egalitarianism also depends on the score function used.
3. In some score functions, in some parameter regimes, egalitarianism and hierarchy are both possible (bistability).

2. Can we infer how agents interact with hierarchies from data?

Yes: we can find most likely parameters and score functions.

Because of the specific form of the probability \(p_{ij}^{(t)}\), this boils down to logistic regression.

Recall that we had this funny looking function that defined a probability of agent \(i\) endorsing agent \(j\):

\[ p_{ij}^{(t)} = \frac{e^{u_{ij}(\mathbf{r}^{(t)})}}{\sum_j e^{u_{ij}(\mathbf{r}^{(t)})}} \]

This lets us assign a likelihood to the observed data as a function of the parameters:

\[\mathcal{L}(\lambda, \beta) = \sum_{t = 0}\sum_{i, j \in \mathcal{N}}a_{ij}^{(t)} \log p_{ij}^{(t)}\]

Method of maximum-likelihood: find \(\lambda\) and \(\beta\) to make this function large.

Data:

Math PhD Exchange¹: University A “endorses” B by hiring a PhD trained at B, over 50 years.
Monk Parakeets²: Parakeet A “endorses” B by losing a fight to B, over 4 observation periods.
Newcomb Fraternity³: Fraternity brother A “endorses” B by stating that they like B on a survey, over a semester (15 weeks).

¹D. Taylor, S. A. Meyers, A. Clauset, M. A. Porter, P. J. Mucha, Eigenvector-based centrality measures for temporal networks. Multiscale Model. Simul. 15, 537–574 (2017).
North Dakota State University Department of Mathematics, Data from “The Mathematics Genealogy Project.” (link)
²E. A. Hobson, S. DeDeo, Social feedback and the emergence of rank in animal society. PLoS Comput. Biol. 11, e1004411 (2015)
³T. Newcomb, The Acquaintance Process (Holt, Reinhard, and Winston, New York, NY, 1961).

Recall that we had this funny looking function that defined a probability of agent \(i\) endorsing agent \(j\):

\[ p_{ij}^{(t)} = \frac{e^{u_{ij}(\mathbf{r}^{(t)})}}{\sum_j e^{u_{ij}(\mathbf{r}^{(t)})}} \]

This lets us assign a likelihood to the observed data as a function of the parameters:

\[\mathcal{L}(\lambda, \beta) = \sum_{t = 0}\sum_{i, j \in \mathcal{N}}a_{ij}^{(t)} \log p_{ij}^{(t)}\]

Method of maximum-likelihood: find \(\lambda\) and \(\beta\) to make this function large.

Data:

Math PhD Exchange¹: University A “endorses” B by hiring a PhD trained at B, over 50 years.
Monk Parakeets²: Parakeet A “endorses” B by losing a fight to B, over 4 observation periods.
Newcomb Fraternity³: Fraternity brother A “endorses” B by stating that they like B on a survey, over a semester (15 weeks).

¹D. Taylor, S. A. Meyers, A. Clauset, M. A. Porter, P. J. Mucha, Eigenvector-based centrality measures for temporal networks. Multiscale Model. Simul. 15, 537–574 (2017).
North Dakota State University Department of Mathematics, Data from “The Mathematics Genealogy Project.” (link)
²E. A. Hobson, S. DeDeo, Social feedback and the emergence of rank in animal society. PLoS Comput. Biol. 11, e1004411 (2015)
³T. Newcomb, The Acquaintance Process (Holt, Reinhard, and Winston, New York, NY, 1961).

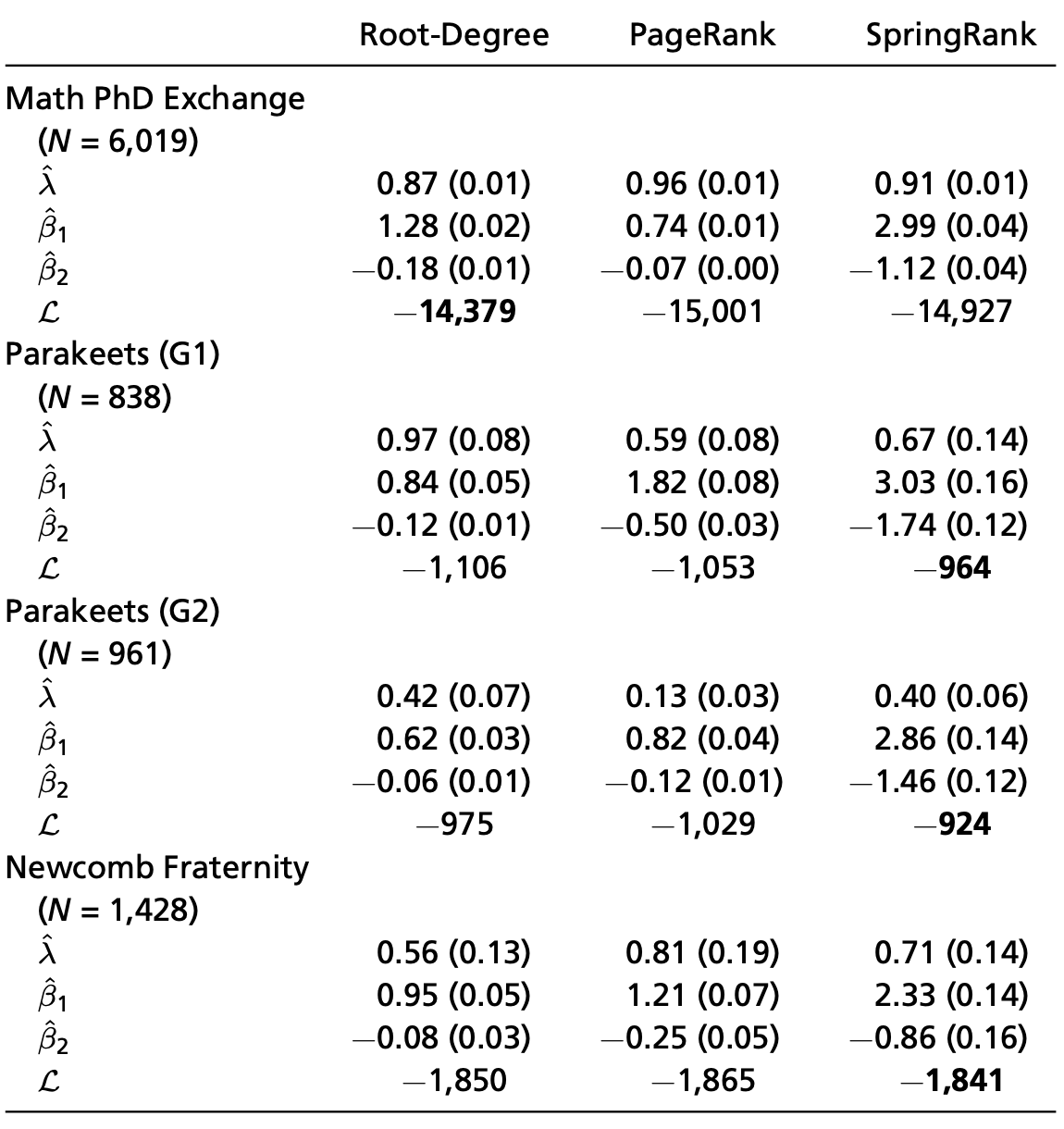
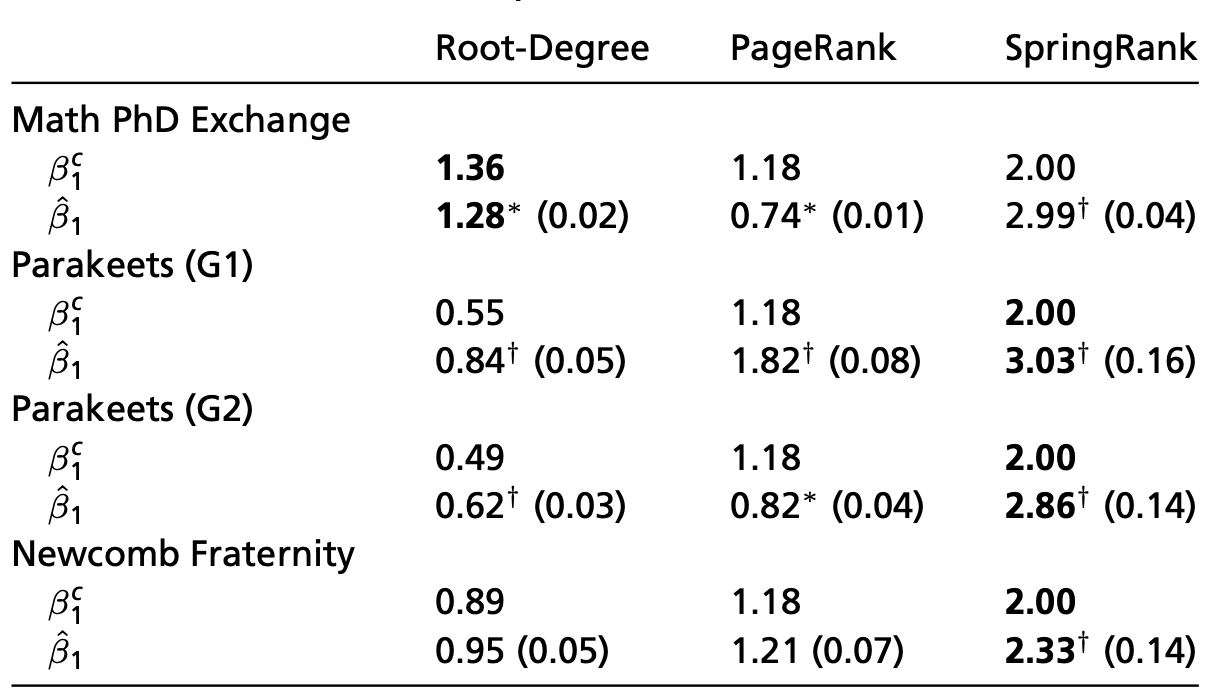
Are we in the hierarchical regime?

Theorem from before: Egalitarianism is stable iff \(\beta_1 < \beta_1^c\), where

\[\beta_1^c = \begin{cases} 2\sqrt{\frac{n}{m}} &\quad \text{Root-Degree} \\ 1/\alpha_p &\quad \text{PageRank} \\ 2 + \alpha_s\frac{n}{m} &\quad \text{SpringRank}. \end{cases}\]

Math PhD exchange: bistable \(-\) both egalitarianism and hierarchy are possible.

Parakeets + Newcomb Frat: hierarchical.

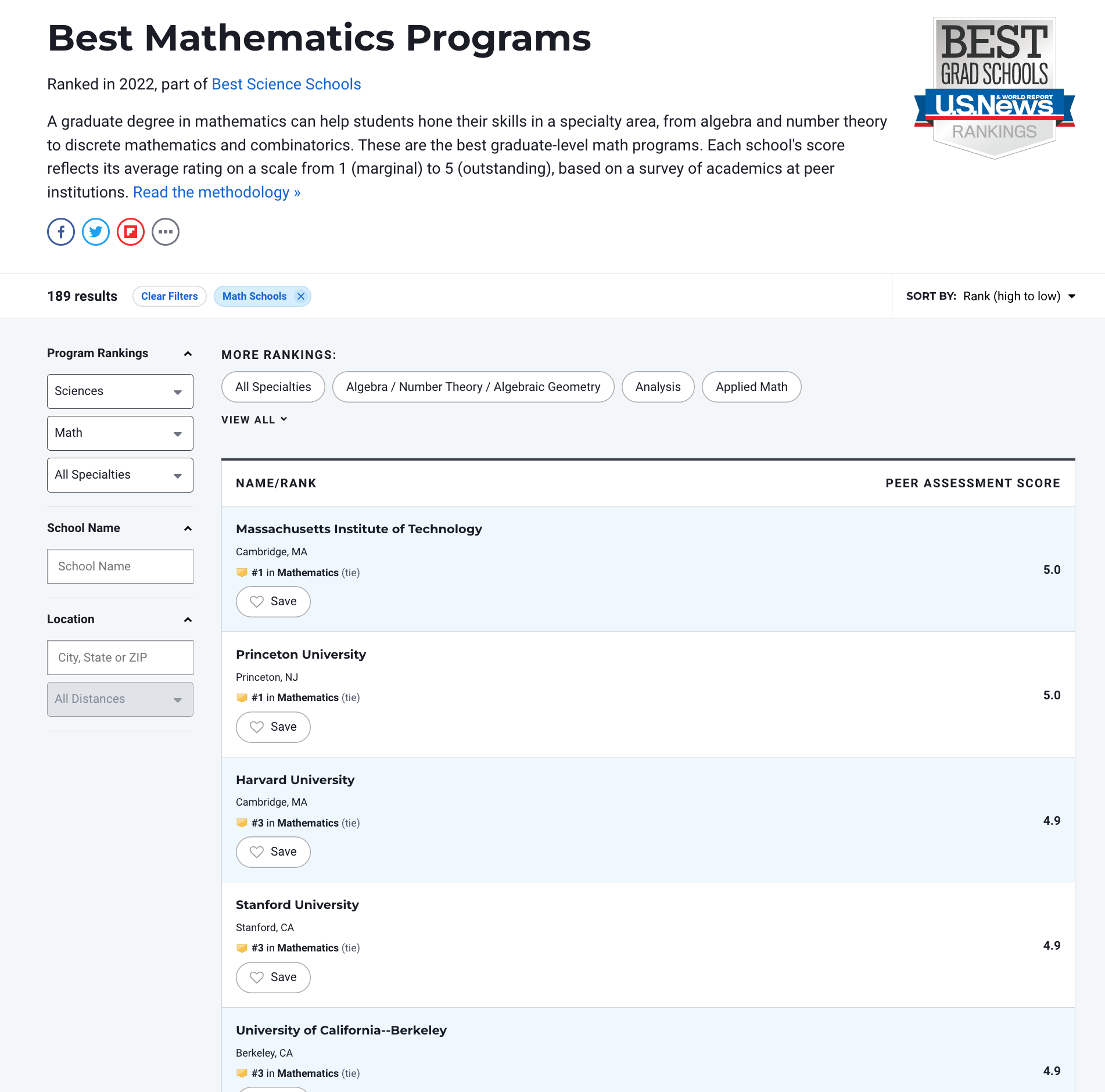
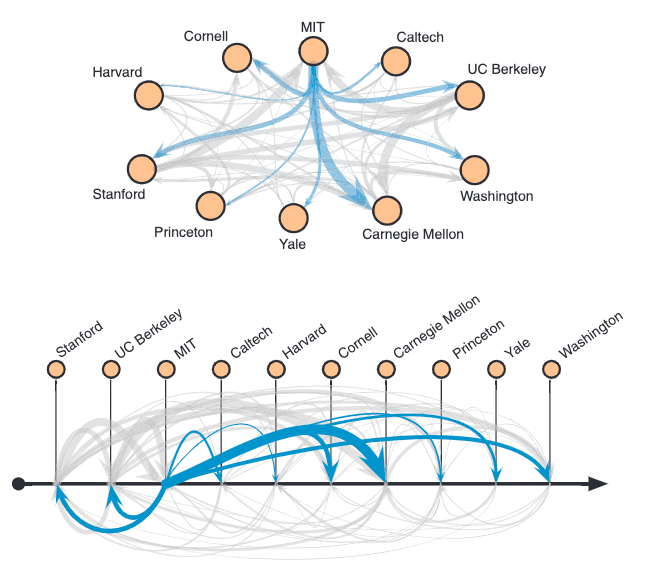
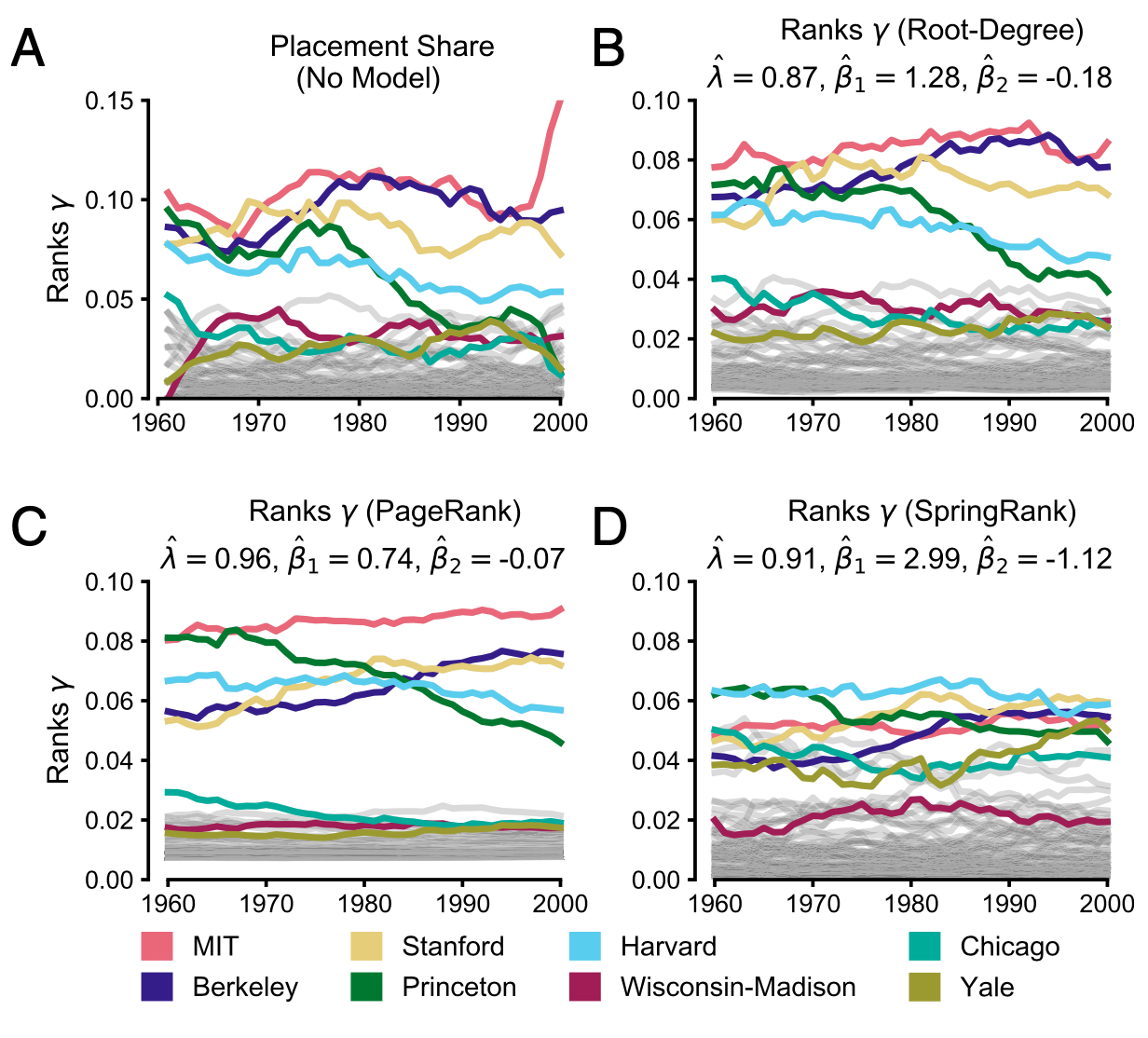
It matters how we compute the ranks!

Placement share, Root-Degree, and PageRank: MIT dominates, esp. recently.

SpringRank: Favors Harvard, Stanford, Princeton, and Berkeley (based on prestigious placements of their graduates).

Different estimates of fluidity in ranks.

Ranks ⟳ Decisions

We wrote a simple math model of hierarchies emerging from feedback loops.

Feedback loops can generate stable hierarchies, even when are no meaningful differences between agents.

Some systems are near criticality: small interventions could help to promote equality and equity.

Two Ways to Start Projects

Idea First

“Here’s a cool idea!
What/who do I need to do in order to achieve this?”

People First

“Here are some people I like!
What cool things can we achieve together?”

I do both of these, but I have the most fun when I start with people.

Reflections on interdisciplinary applied math being a human in science

Find people worth your trust, and trust them.

Be thankful, and say so.

Check in often.

Work with your heart, not just your brain.

Take time to see things from multiple angles.

Laugh. A lot.

Thanks!

Awesome Collaborators

Mari Kawakatsu
UPenn and Princeton
Nicole Eikmeier
Grinnell
Dan Larremore
CU Boulder

Complex Networks Winter Workshop 2019

And Most Importantly…